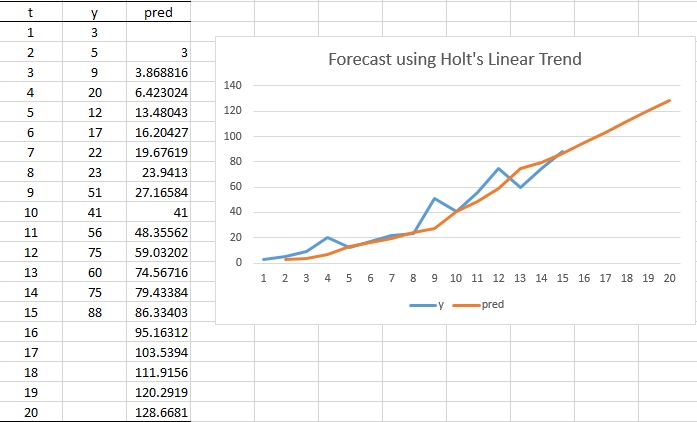
霍特林线性趋势法(Holt's linear trend method)是一种时间序列预测方法,它适用于具有线性趋势的数据。该方法由 Charles C. Holt 在 1957 年提出,旨在扩展简单指数平滑法以处理具有趋势的时间序列数据。
- 水平分量:用于描述时间序列的基础水平或均值。
- 趋势分量:体现数据随时间呈现出的线性变化趋势。
该方法通过对历史数据的分析,来估计水平分量和趋势分量,并基于这些估计对未来的值进行预测。
例如,假设我们有一组销售量的时间序列数据,通过霍特林线性趋势法,可以确定销售量的大致平均水平以及销售量增长或减少的趋势。然后利用这些信息来预测未来几个时期的销售量可能处于什么范围。
它的优点包括相对简单易用,能够较好地处理具有线性趋势的数据。然而,它也有一定局限性,比如对于非线性趋势或复杂波动的数据可能不太适用。
一、组成部分
预测方程:用于生成未来值的预测。
水平方程:用于平滑时间序列数据,反映其基础水平。
趋势方程:用于平滑时间序列的趋势部分。
表达式如下:
「」
二、分析过程
1. 理解数据特性:
- 在开始之前,首先需要理解时间序列数据的特性,包括是否存在趋势、季节性等。
2. 数据准备:
- 清洗数据,处理缺失值或异常值。
- 绘制时间序列图,直观观察数据趋势。
3. 选择平滑参数:
- 选择适当的平滑参数α 和 β。这些参数决定了模型对新数据的响应速度和对历史数据的重视程度。
4. 初始化模型参数:
- 为模型选择合适的初始值,如初始水平ℓ 1和初始趋势b1。
5. 计算平滑值:
- 使用水平方程和趋势方程迭代计算每个时间点的平滑水平 ℓ t和平滑趋势 bt 。
6. 生成预测:
- 根据预测方程,使用当前的平滑水平和趋势来生成未来时间点的预测值。
7. 评估模型性能:
- 使用诸如均方误差(MSE)或均方根误差(RMSE)等统计指标来评估模型的预测性能。
8. 调整模型参数:
- 根据模型评估结果,可能需要调整平滑参数以改进预测准确性。
9. 进行预测:
- 使用调整后的模型进行未来值的预测。
10. 模型验证:
- 将模型预测的结果与实际发生的值进行比较,验证模型的准确性和可靠性。
11. 报告和解释:
- 准备预测报告,解释模型的选择、参数的调整以及预测结果。
12. 监控和更新:
- 在实际应用中,需要定期监控模型的表现,并根据新的数据更新模型参数。
霍特林线性趋势法的关键在于选择合适的平滑参数,并通过迭代计算来捕捉时间序列数据中的线性趋势。
三、应用场景
霍特林线性趋势法适用于那些显示出明显线性趋势的数据集。以下是一些典型的应用场景:
1. 经济指标预测:在宏观经济分析中,经常需要预测经济指标,如GDP增长率、失业率、通货膨胀率等,这些指标往往表现出一定的趋势性。
2. 销售预测:企业可以利用霍特林线性趋势法来预测产品或服务的未来销售量,帮助制定生产计划和库存管理。
3. 金融市场分析:在金融市场中,分析师经常使用时间序列方法来预测股票价格、利率、汇率等,并制定投资策略。
4. 库存管理:通过预测产品需求的趋势,企业可以更有效地管理库存,减少库存积压或缺货的风险。
5. 资源分配:政府或企业可以利用趋势预测来合理分配资源,如能源、交通设施的规划等。
6. 季节性产品需求预测:对于具有明显季节性波动的产品,如冬季服装或节日商品,霍特林线性趋势法可以帮助预测不同时间段的需求。
7. 网络流量分析:互联网服务提供商可能会使用此方法来预测网络流量趋势,以便更好地规划网络带宽和服务器资源。
8. 房地产价格趋势:房地产行业可以利用此方法来分析和预测房价走势,为投资决策提供依据。
9. 医疗资源规划:卫生部门可以通过分析患者就诊趋势来预测未来对医疗资源的需求,从而进行更有效的资源规划。
10. 环境监测:环境科学家可能会使用时间序列分析来监测和预测环境指标,如污染水平、气候变化趋势等。
霍特林线性趋势法因其简单性和有效性,在需要预测具有线性趋势的时间序列数据时被广泛应用。