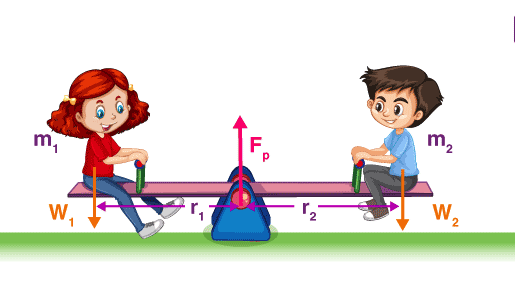
平衡分析法(Equilibrium Analysis)用于确定系统在不同因素影响下达到平衡状态的条件,是一种研究系统在多个变量相互作用下达到稳定状态的方法。平衡分析法的核心在于识别系统中的平衡点,即系统内部的力或过程相互抵消,导致系统宏观性质保持不变的状态。平衡点的定义:系统达到一个状态,其中所有内部过程的速率相互抵消,系统参数(如温度、压力、浓度等)不随时间变化。
一、原理
1. 系统稳定性:平衡分析法首先假设系统处于或趋向于一个稳定状态,即系统参数不随时间发生显著变化。
2. 相互作用:系统内的各个组成部分或变量之间存在相互作用,这些相互作用决定了系统的行为。
3. 平衡条件:系统达到平衡状态时,内部的力或过程相互抵消,没有净的变化发生。例如,在化学反应中,正反应和逆反应的速率相等。
4. 动态平衡:即使系统看起来是静止的,实际上可能存在动态平衡,即系统内部的某些过程仍在进行,但总体上没有净的变化。
5. 数学模型:通过建立数学模型来描述系统的状态和变量之间的关系。这些模型可以是代数方程、微分方程或差分方程等。
6. 求解平衡点:使用数学方法求解这些方程,找到系统平衡时的变量值。这些值通常被称为平衡常数或平衡浓度。
7. 敏感性分析:分析系统对不同参数变化的敏感性,了解哪些因素对系统平衡状态有较大影响。
8. 应用与验证:将平衡分析的结果应用于实际问题中,并与实验数据或观测结果进行比较,以验证模型的准确性和适用性。
二、分析过程
1. 确定系统边界:首先定义分析的系统范围,明确系统的输入和输出,以及系统与外界的交互。
2. 识别系统变量:确定影响系统平衡状态的关键变量,如温度、压力、浓度、流量等。
3. 建立平衡方程:根据物理、化学或经济原理,建立描述系统平衡状态的数学方程。这些方程可能包括质量守恒、能量守恒、动量守恒等。
4. 确定初始条件:设定系统开始分析时的初始状态,包括各变量的初始值。
5. 求解平衡点:使用数学方法(如代数方法、微分方程求解等)求解平衡方程,找到系统达到平衡时的变量值。
6. 稳定性分析:评估系统在平衡点附近的稳定性。这可能包括线性稳定性分析,即分析系统对小扰动的响应。
7. 敏感性分析:研究系统平衡状态对关键参数变化的敏感性,识别影响系统平衡的主要因素。
8. 模拟和预测:使用平衡分析的结果进行模拟,预测系统在不同条件下的行为。
9. 验证和调整:将平衡分析的预测结果与实验数据或实际观测结果进行比较,验证模型的准确性。根据需要调整模型参数或假设。
10. 优化和决策支持:利用平衡分析的结果进行系统优化,为决策提供支持。
11. 报告和文档:编写分析报告,记录分析过程、结果和结论,以及任何推荐的行动方案。
平衡分析法的分析过程需要综合考虑系统的物理特性、化学性质、经济因素等多种因素,以确保分析的全面性和准确性。通过这一过程,可以更好地理解和控制复杂系统的行为。
三、应用场景
1. 经济学:在经济学中,平衡分析法用于研究市场供求关系、价格形成机制以及经济政策对市场的影响。
2. 企业管理:企业可以运用平衡分析法进行成本效益分析、盈亏平衡点分析,以及优化生产和运营策略。
3. 宏观经济规划:政府和决策者使用平衡分析法来制定和评估宏观经济政策,如税收、财政支出和货币政策。
4. 环境科学:在环境领域,平衡分析法可以帮助评估资源的使用和分配,以及环境政策对生态系统平衡的影响。
5. 能源领域:平衡分析法用于能源需求预测、能源资源的合理分配和能源政策的制定。
6. 金融投资:金融领域中,平衡分析法用于评估资产价格、风险管理和投资组合的优化。
7. 农业经济:在农业领域,平衡分析法可以用于评估农业生产力、资源配置和农产品市场分析。
8. 教育和研究:教育机构和研究人员使用平衡分析法来研究各种社会经济现象和政策效果。
9. 国际关系:平衡分析法也可用于分析国际政治经济关系,如贸易平衡、国际投资等。
10. 健康医疗:在医疗领域,平衡分析法可以用于评估医疗资源的分配和医疗服务的供需关系。
平衡分析法作为一种分析工具,其核心在于评估不同因素之间的相互作用及其对系统平衡状态的影响,从而为决策提供依据。
平衡分析法广泛应用于化学平衡、经济市场分析、生态平衡、物理平衡状态等领域。通过这种方法,可以预测和控制系统的行为,优化系统性能。