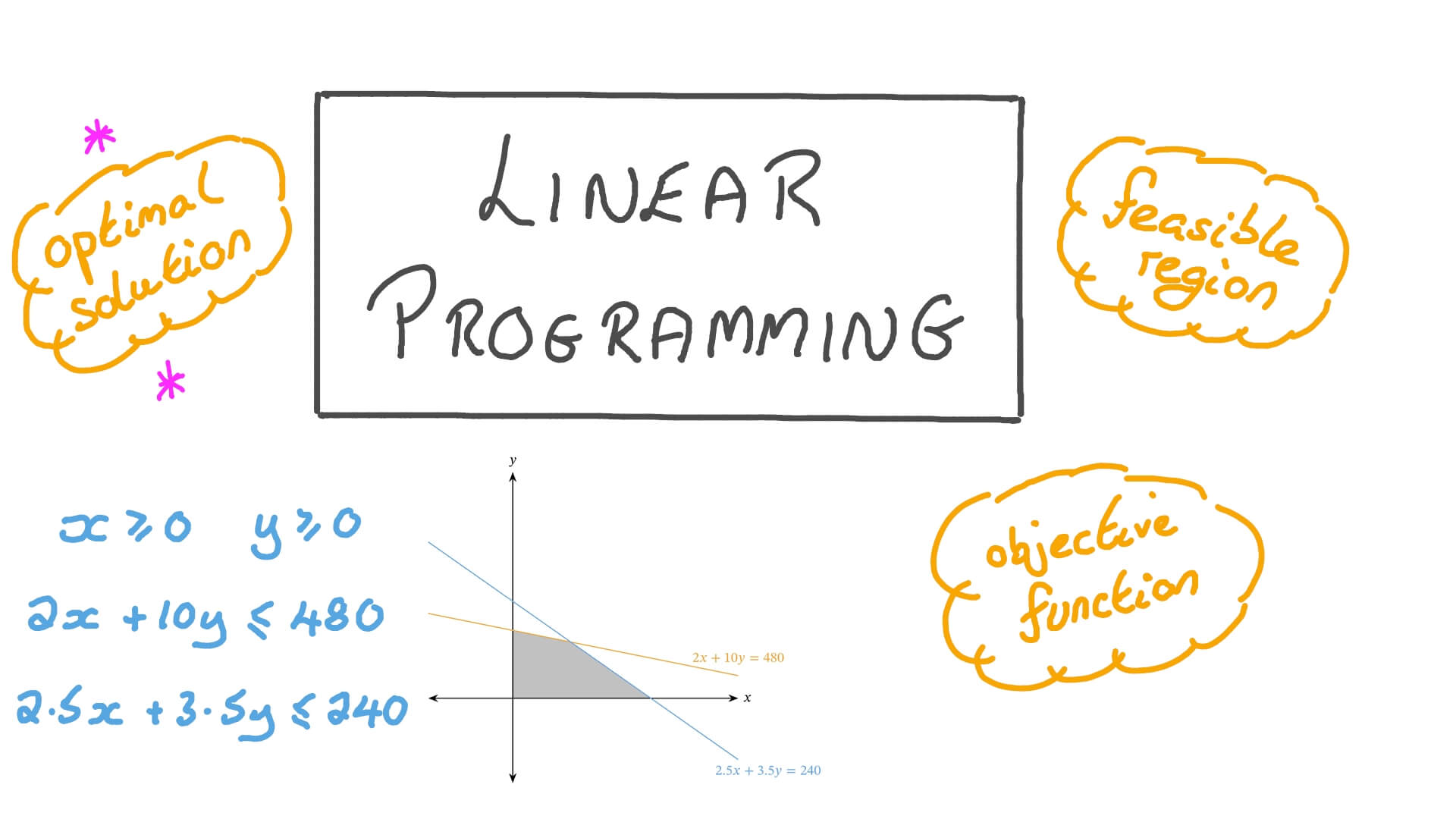
线性规划(Linear Programming,LP)是一种数学方法和算法,用于在一组线性不等式的约束下,找到线性目标函数的最大值或最小值。它是运筹学的一个重要分支,广泛应用于经济学、商业、工程和其他领域。
一、基本概念
线性规划问题通常可以表示为以下形式:
【】
二、分析过程
线性规划的分析过程通常包括以下几个步骤:
1. 问题定义:
- 明确问题的目标和约束条件。
- 确定目标函数,这是需要优化(最大化或最小化)的线性函数。
- 确定约束条件,这些是问题中的线性不等式或等式。
2. 模型建立:
- 用数学表达式来表示目标函数和约束条件。
- 将问题转化为标准的线性规划形式
3. 求解前的准备:
- 检查问题的可行性,确保至少存在一个可行解。
- 对问题进行初步分析,比如通过图形方法(对于二维或三维问题)来获得问题的直观理解。
4. 选择求解方法:
- 根据问题的特点选择合适的求解算法,如单纯形法、内点法、对偶方法等。
5. 求解:
- 使用所选的求解方法和工具(如软件或编程实现)来求解线性规划问题。
6. 结果分析:
- 分析求解结果,确定最优解或最优解集。
- 检查解的稳定性和对参数变化的敏感性。
7. 灵敏度分析:
- 评估目标函数和约束条件变化对最优解的影响。
- 进行灵敏度分析可以帮助了解解的鲁棒性。
8. 后处理:
- 根据求解结果进行决策支持,可能包括调整策略或计划。
- 将结果应用于实际问题,进行实施和监控。
9. 文档记录:
- 记录整个分析过程,包括模型建立、求解方法选择、结果分析和灵敏度分析等,以备复查或作为决策支持的依据。
10. 验证和测试:
- 对模型和结果进行验证,确保它们在实际应用中是有效的。
- 可能需要进行测试或模拟来验证模型的预测能力。
线性规划的分析过程是一个迭代和多阶段的过程,可能需要多次调整模型和求解方法以获得满意的结果。
三、求解方法
线性规划问题可以通过多种方法求解,包括图形方法、单纯形法、对偶单纯形法、内点法等。这些方法各有优缺点,适用于不同类型的问题和规模。
1. 图形方法:适用于两个变量的线性规划问题,通过图形直观地找到最优解。
2. 单纯形法:一种迭代算法,适用于大规模问题,通过逐步改变基可行解来寻找最优解。
3. 对偶单纯形法:单纯形法的变体,用于求解原问题的对偶问题,有时可以更高效地找到原问题的解。
4. 内点法:一种基于优化问题内部点的算法,通常用于大规模问题,收敛速度快但可能需要更复杂的数学处理。
四、应用场景
1. 生产计划:企业可以利用线性规划来确定不同产品的生产量,以满足市场需求同时最大化利润。
2. 资源分配:在有限的资源下,如何分配资源以完成多个项目或任务,例如资金、人力或原材料的分配。
3. 运输问题:确定货物从多个供应点到多个需求点的最有效运输方式,以最小化运输成本。
4. 混合问题:在化工、食品加工等行业中,确定不同原料的混合比例,以生产出符合特定要求的产品。
5. 网络流问题:在网络(如交通网络、通信网络)中优化资源的流动,例如数据传输、车辆调度等。
6. 投资组合优化:在金融领域,线性规划可以帮助投资者在风险和回报之间找到平衡,构建最优的投资组合。
7. 设施选址:确定新工厂或仓库的最佳位置,考虑到成本、运输、市场需求等因素。
8. 农业规划:在农业生产中,决定不同作物的种植面积,以最大化收益或满足特定的生产目标。
9. 能源管理:在能源领域,线性规划可以用来优化能源的生产、分配和消费。
10. 供应链管理:优化供应链中的库存水平、生产计划和物流,以减少成本和提高效率。
11. 环境规划:在环境政策制定中,线性规划可以用来评估不同政策对资源使用和环境影响的效果。
12. 健康保健资源分配:在医疗保健领域,线性规划可以帮助医院或卫生组织合理分配医疗资源,如床位、医护人员和医疗设备。
13. 教育规划:在教育领域,线性规划可以用于优化课程安排、教室分配和教师资源配置。
14. 军事物流:在军事领域,线性规划可以用于优化物资的分配和运输,确保部队的有效补给。
15. 公共工程:在公共工程项目中,线性规划可以帮助决策者在预算限制下,合理分配资金和资源。
线性规划的应用场景非常广泛,几乎涵盖了所有需要在多个约束条件下进行优化决策的领域。通过合理运用线性规划,可以显著提高决策的效率和效果。
五、软件工具
线性规划问题可以通过多种软件工具来求解,以下是一些常见的线性规划软件工具:
1. Excel Solver:Excel中的求解器可以解决一些基本的线性规划问题,适用于教育和小型项目。
2. LINDO:一个商业软件,提供了一个用户友好的界面和强大的求解能力,适用于多种类型的优化问题。
3. CPLEX:由IBM开发,是一个高效的商业线性规划求解器,广泛应用于工业和学术研究中。
4. Gurobi:一个高性能的商用优化求解器,支持多种类型的优化问题,包括线性规划。
5. GAMS:高级数学系统,是一个用于建模和求解大规模优化问题的软件平台,支持线性规划等多种优化技术。
6. SCIP:一个开源的混合整数规划求解器,由德国ZIB研究所开发,也适用于线性规划问题。
7. OR-Tools:谷歌开发的开源软件套件,提供了多种优化算法,包括线性规划求解器。
8. PuLP:一个Python库,可以用于定义和求解线性规划问题,支持多种后端求解器。
9. CVXPY:一个Python优化库,专门用于解决凸优化问题,包括线性规划。
10. scipy.optimize.linprog:Python的scipy库中的函数,可以解决一些基本的线性规划问题。
11. LP_Solve:一个开源的线性规划求解器,适用于多种操作系统。
12. GLPK:GNU线性规划工具包,是一个开源的线性规划求解器,可以在多种操作系统上使用。
这些工具各有特点,用户可以根据自己的需求和偏好选择合适的软件进行线性规划问题的求解。