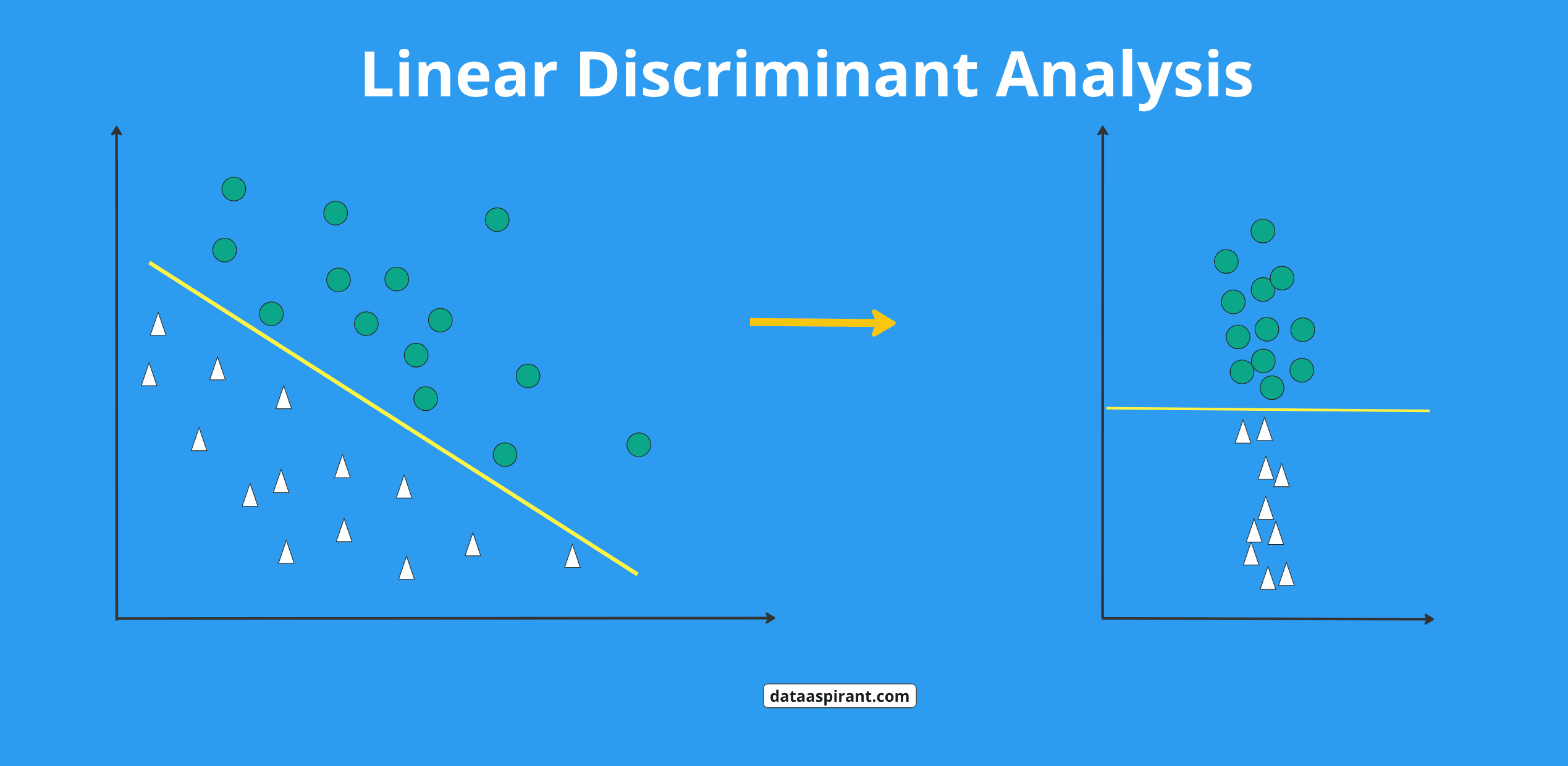
线性判别分析(Linear Discriminant Analysis,简称LDA)是一种统计学方法,用于发现数据中的模式并对其进行分类。它特别适用于监督学习,尤其是在分类问题中。LDA的目标是找到一个线性组合的特征,这有助于将不同的类别分开,从而提高分类器的性能。
一、基本原理
LDA的核心思想是最大化类别间的分离度(类间方差)和最小化类别内的分离度(类内方差)。具体来说,LDA通过以下步骤实现:
1. **计算均值**:对于每个类别,计算其数据点的均值。
2. **计算散布矩阵**(Scatter Matrices):
- **类内散布矩阵**(Within-class Scatter Matrix):计算所有类别的均值和每个数据点之间的距离,然后对所有类别求和。
- **类间散布矩阵**(Between-class Scatter Matrix):计算所有类别均值和总均值之间的距离,然后对所有类别求和。
3. **特征选择**:通过求解广义特征值问题(Generalized Eigenvalue Problem),找到那些对应于最大特征值的特征向量。这些特征向量定义了数据的降维方向,即LDA特征空间。
4. **降维**:将原始数据投影到选定的特征向量上,得到降维后的数据。
二、应用场景
LDA可以用于:
- **分类**:通过找到最佳的投影方向,LDA可以提高分类器的准确性。- **降维**:在进行分类之前,减少数据的维度,以简化模型并减少计算成本。
线性判别分析(LDA)由于其在分类和降维方面的能力,被广泛应用于多种商业场景中。
1. **信用评分**:银行和金融机构使用LDA来分析客户的信用风险,通过分析客户的各种特征(如收入、负债、历史还款记录等),LDA可以帮助金融机构预测客户未来偿还贷款的可能性。
2. **市场细分**:企业可以利用LDA对客户进行细分,以便更好地理解不同客户群体的特征,并据此制定更为精准的营销策略。
3. **欺诈检测**:在信用卡交易和保险索赔中,LDA可以用来识别可能的欺诈行为。通过分析历史数据,LDA可以揭示欺诈行为的特征模式。
4. **客户满意度分析**:服务行业可以应用LDA来分析客户反馈,识别影响客户满意度的关键因素,并据此改进服务。
5. **产品推荐系统**:在线零售商和流媒体服务可以使用LDA分析用户行为和偏好,以提供个性化的产品或内容推荐。
6. **医疗诊断**:在医疗领域,LDA可以帮助医生分析病人的症状和检查结果,从而辅助诊断疾病。
7. **新闻媒体分析**:LDA可以用于分析新闻报道,识别报道中的主要主题,帮助媒体机构了解公众关注点和社会动态。
8. **人力资源管理**:企业可以利用LDA分析员工的工作表现和行为特征,以预测员工的离职倾向或晋升潜力。
9. **股票市场分析**:在金融领域,LDA可以用于分析和预测股票价格走势,帮助投资者做出更明智的投资决策。
10. **社会媒体监控**:企业可以使用LDA来分析社交媒体上的讨论,识别舆论趋势,监控品牌声誉。
这些应用场景展示了LDA在商业智能、风险管理、客户关系管理、市场研究和产品开发等多个领域的潜力。通过LDA,企业和组织能够从大量数据中提取有价值的信息,以支持决策制定和战略规划。
三、优缺点
**优点**:
- **简单**:LDA是一种简单且计算效率高的方法。
- **有效**:在许多情况下,LDA可以显著提高分类器的性能。
- **可解释性**:LDA的特征向量具有明确的统计学意义,易于解释。
**缺点**:
- **线性假设**:LDA假设类别是线性可分的,这在实际应用中可能不总是成立。
- **特征数量**:如果特征数量大于样本数量,LDA可能会失败,因为它需要足够的数据来估计散布矩阵。
- **类别数量**:对于不平衡的数据集,LDA可能不会表现得很好,因为它依赖于类别均值和方差。
四、实现
LDA可以通过多种方式实现,包括传统的统计软件包(如R、Python的scikit-learn库)和机器学习框架。
在Python中,可以使用`scikit-learn`库中的`LinearDiscriminantAnalysis`类来实现LDA:
```python
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
lda = LinearDiscriminantAnalysis()
lda.fit(X, y) # X是特征数据,y是标签
```
通过这种方式,LDA可以很容易地集成到机器学习工作流程中。