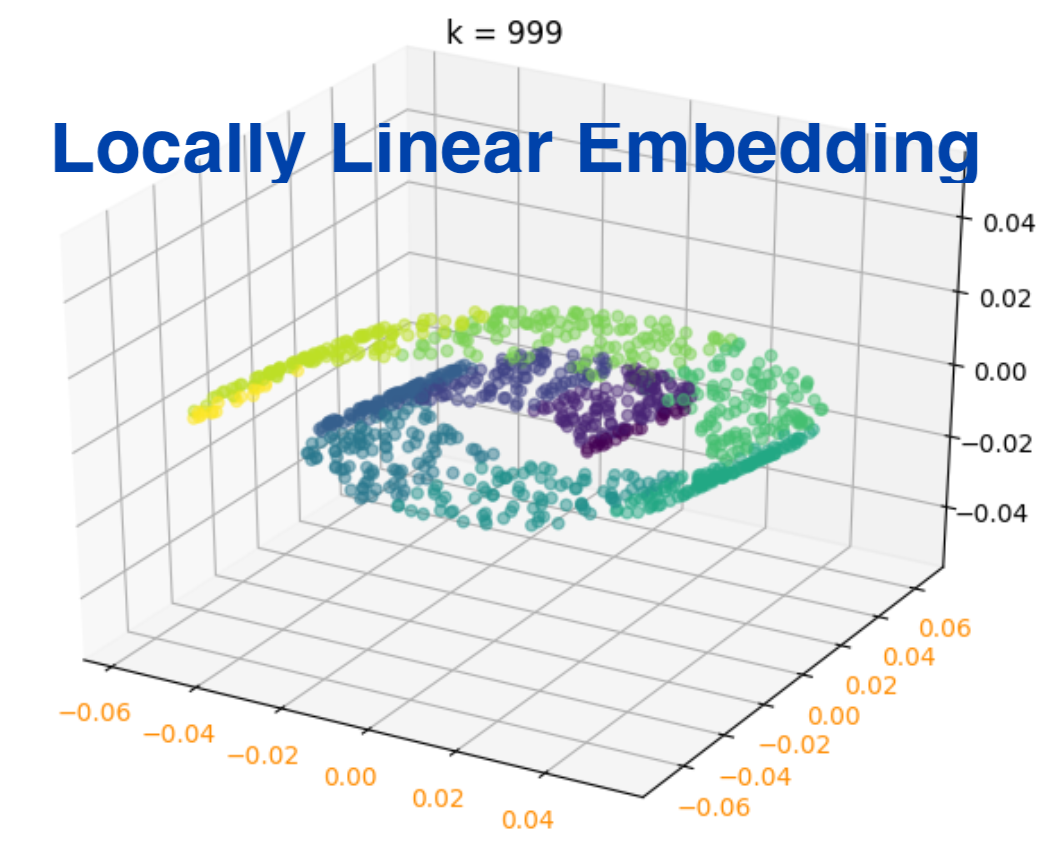
局部线性嵌入(Locally Linear Embedding,LLE)是一种用于维数约减的非线性技术,由Sam Roweis和Lawrence Saul于2000年提出。LLE的目标是在低维空间中保持数据点之间的局部邻域结构,同时尽可能保持全局结构。
一、LLE的主要思想
1. **局部线性重构**:LLE假设在高维空间中的每个数据点都可以由其近邻的线性组合来近似。这意味着在局部邻域内,数据点之间是线性相关的。
2. **保持局部距离**:在低维空间中,LLE试图保持数据点与其近邻之间的距离,从而保持局部结构。
3. **全局结构的保持**:虽然LLE主要关注局部结构,但它也试图在一定程度上保持全局结构。
二、LLE的步骤
1. **选择近邻**:对于高维空间中的每个数据点,选择其k个最近邻。
2. **构建局部线性模型**:对于每个数据点,找到一组权重,使得该点是其近邻的线性组合,并且这些权重反映了点之间的局部关系。
3. **优化目标函数**:构建一个目标函数,该函数最小化原始高维空间中点与由其近邻线性组合得到的点之间的距离,同时在低维空间中保持这些距离。
4. **求解新坐标**:通过求解优化问题,找到每个数据点在低维空间中的坐标。
三、LLE的应用
LLE可以应用于多种场景
- **数据可视化**:通过将高维数据映射到二维或三维空间,以便于可视化。
- **特征提取**:作为特征提取技术,用于机器学习任务。
- **图像处理**:用于图像分析和图像分割。
- **生物信息学**:用于基因表达数据的分析。
以下是一些可能的商业应用案例:
1. **客户细分**:通过分析客户数据,LLE可以帮助企业识别不同的客户群体,并了解他们的行为模式和偏好,从而提供更加个性化的服务或产品。
2. **产品推荐系统**:在电子商务中,LLE可以用于分析用户行为和产品特性,以发现潜在的产品关联和用户偏好,进而提供定制化的产品推荐。
3. **市场趋势分析**:LLE能够揭示市场数据中的复杂模式和趋势,帮助企业理解市场动态,预测未来趋势,并制定相应的市场策略。
4. **图像识别与处理**:在零售业中,LLE可以用于图像识别系统,帮助自动化库存管理和商品分类,提高效率。
5. **风险管理**:在金融行业,LLE可以用于分析和识别潜在的风险因素,比如信用风险评估,通过分析客户数据来预测违约概率。
6. **生物信息学**:在医疗健康领域,LLE可以用于基因表达数据分析,帮助识别疾病标志物,促进个性化医疗的发展。
7. **供应链优化**:LLE可以用于分析供应链数据,优化库存管理,减少物流成本,并提高供应链的响应速度和灵活性。
8. **社交媒体分析**:企业可以利用LLE分析社交媒体数据,了解消费者情绪和舆论趋势,从而制定有效的公关和营销策略。
9. **客户服务与支持**:通过分析客户服务日志,LLE可以帮助企业识别常见问题和客户需求,优化客户服务流程。
10. **网络安全**:LLE可以用于网络安全领域,通过分析网络流量数据,识别异常行为和潜在的安全威胁。
商业应用的成功实施还需要考虑数据的质量、算法的适应性以及业务目标等因素。
四、LLE的局限性:
- **计算复杂性**:LLE算法在计算上相对复杂,尤其是当数据集很大时。
- **参数选择**:选择合适的近邻数k和低维空间的维数需要仔细考虑,这可能会影响结果的质量。
- **全局结构**:虽然LLE试图保持全局结构,但在某些情况下可能不如其他方法有效。
五、Python应用
局部线性嵌入(LLE)是一种流行的降维技术,它在Python中可以通过`scikit-learn`库来实现。
1. **安装scikit-learn**:如果你还没有安装`scikit-learn`,可以通过pip安装:
```bash
pip install scikit-learn
```
2. **导入库**:导入`scikit-learn`中的`LocallyLinearEmbedding`类。
```python
from sklearn.manifold import LocallyLinearEmbedding
```
3. **准备数据**:准备你的数据集,通常是一个特征矩阵`X`,其中每行代表一个样本,每列代表一个特征。
4. **选择参数**:设置LLE的参数,如近邻数`n_neighbors`和降维后的维数`n_components`。
5. **训练模型**:使用数据训练LLE模型。
6. **转换数据**:使用训练好的模型将高维数据转换到低维空间。
下面是一个简单的示例代码,展示了如何使用`scikit-learn`进行LLE:
```python
from sklearn.manifold import LocallyLinearEmbedding
from sklearn.datasets import make_swiss_roll
import matplotlib.pyplot as plt
# 生成模拟数据
X, color = make_swiss_roll(n_samples=1000)
# 初始化LLE对象
lle = LocallyLinearEmbedding(n_neighbors=10, n_components=2, method='standard')
# 执行LLE降维
X_transformed = lle.fit_transform(X)
# 可视化降维后的数据
plt.scatter(X_transformed[:, 0], X_transformed[:, 1], c=color)
plt.show()
```
在这个示例中,我们首先生成了一个模拟的瑞士卷数据集,然后使用LLE将其从高维空间映射到2维空间,并使用matplotlib库进行可视化。
请注意,`n_neighbors`参数的选择对LLE的性能有很大影响。通常,你需要根据数据集的特性来调整这个参数。`method`参数可以是`'standard'`, `'hessian'`, `'modified'`或`'ltsa'`,它们代表不同的LLE变体。
此外,还有其他参数可以调整,例如正则化系数`reg`,特征分解方法`eigen_solver`和邻居搜索算法`neighbors_algorithm`。这些参数可以帮助优化LLE的性能和适应不同的数据集。
总之,LLE是一种强大的工具,可以帮助我们理解和可视化高维数据集,但它需要仔细的参数调整和对数据特性的深入理解。