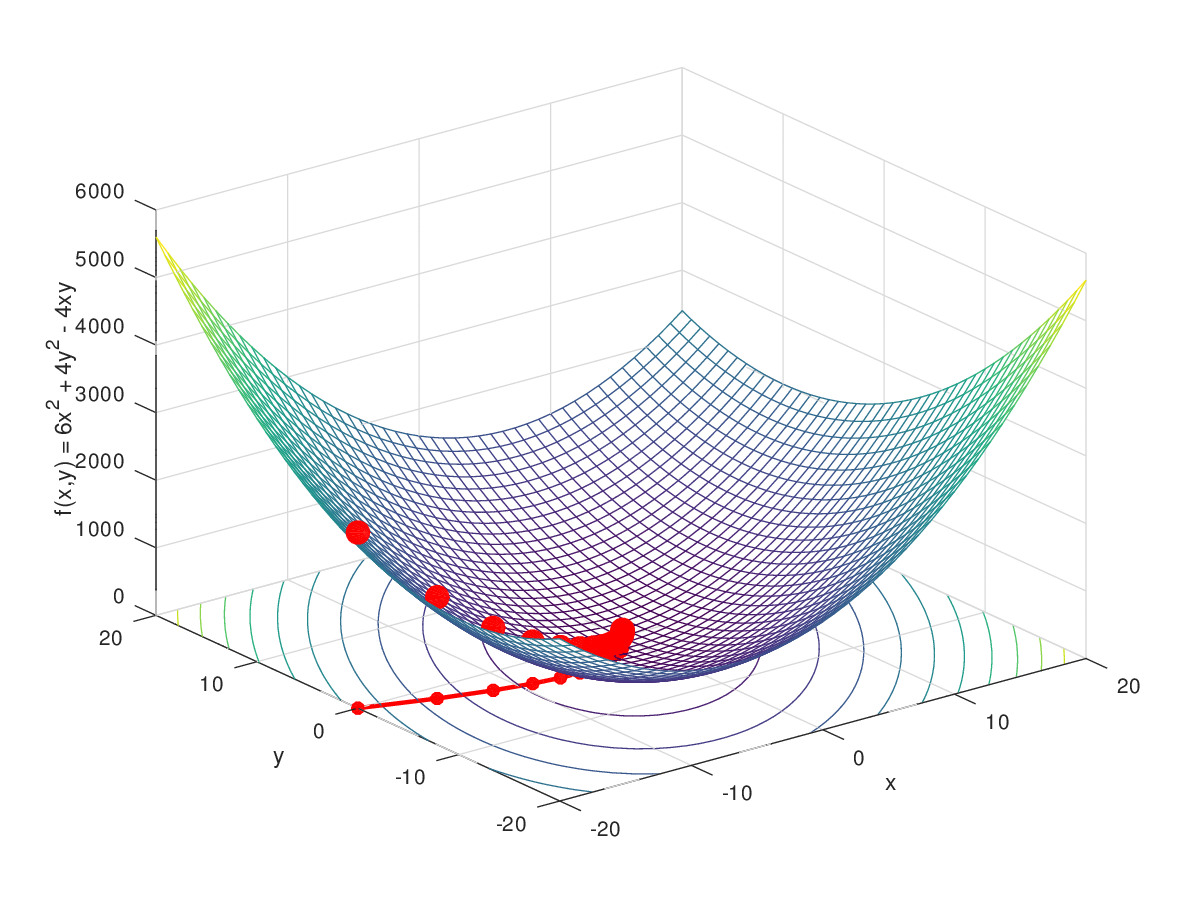
梯度下降(Gradient Descent)是一种优化算法,用于最小化一个函数,通常在机器学习和人工智能中用于找到函数的局部最小值。这个函数通常是损失函数,它衡量了模型预测值与实际值之间的差异。梯度下降的核心思想是迭代地调整参数,以减少损失函数的值。
用于求解无约束优化问题的迭代算法,特别常用于机器学习中的参数估计问题。其基本思想是,通过迭代地调整参数,沿着函数的负梯度方向寻找函数的局部最小值。
一、梯度下降算法的步骤
【】
二、梯度下降的变体:
1. 批量梯度下降(Batch Gradient Descent):每次迭代使用整个数据集来计算梯度。
2. 随机梯度下降(Stochastic Gradient Descent, SGD):每次迭代只使用一个训练样本来计算梯度。
3. 小批量梯度下降(Mini-batch Gradient Descent):每次迭代使用一小部分数据来计算梯度,介于批量和随机之间。
三、梯度下降算法的关键点
- 学习率:学习率 α 是一个超参数,需要根据问题进行调整。如果学习率太大,可能会跳过最小值甚至发散;如果学习率太小,则收敛速度会很慢。
- 收敛性:梯度下降算法不保证找到全局最小值,有时可能会陷入局部最小值或鞍点。
- 梯度计算:梯度的计算需要对目标函数进行微分,这在某些情况下可能非常复杂。
- 选择初始点:不同的初始点可能导致收敛到不同的局部最小值。
- 超参数调整:除了学习率,还有其他超参数,如动量(Momentum)、自适应学习率等,可以通过这些技术来改进梯度下降的性能。
四、应用:
梯度下降在机器学习中非常广泛,尤其是在训练线性回归、逻辑回归、神经网络等模型时。通过最小化损失函数,梯度下降可以帮助我们找到模型的最佳参数。
以下是一些具体的商业应用案例:
1. 推荐系统:电商平台和社交媒体平台经常使用梯度下降来优化推荐算法,通过分析用户行为和偏好来提供个性化推荐。
2. 广告投放:在线广告平台利用梯度下降算法优化广告投放策略,以实现更高的点击率和转化率。
3. 股票市场分析:金融机构使用梯度下降来预测股票价格,优化投资组合,以及进行风险管理。
4. 供应链优化:企业通过梯度下降算法优化库存管理、物流和配送路线,以降低成本并提高效率。
5. 客户关系管理(CRM):公司使用梯度下降来分析客户数据,预测客户流失,以及制定客户保留策略。
6. 定价策略:企业可以利用梯度下降算法分析市场需求和竞争对手定价,以确定最优产品价格。
7. 图像识别:在零售业中,图像识别技术可以用于自动结账系统,其中梯度下降算法帮助提高识别准确率。
8. 自然语言处理:在客户服务领域,梯度下降算法可以用于优化聊天机器人的性能,提高自动回复的准确性。
9. 机器翻译:在国际贸易和全球化业务中,梯度下降算法被用来优化机器翻译系统,提高翻译质量。
10. 语音识别:在呼叫中心和智能助手中,梯度下降算法用于提高语音识别系统的准确性和响应速度。
梯度下降算法之所以在商业领域如此流行,是因为它能够处理大规模数据集,并且能够找到复杂函数的局部最小值,这对于优化商业决策和提高运营效率至关重要。
五、Python应用
以下是一些基本的Python应用示例:
1. 简单线性回归
假设我们有一组数据点,我们想要找到一个直线(线性模型),它最好地拟合这些点。我们可以使用梯度下降来优化线性回归模型的参数。
```python
import numpy as np
假设的数据点
X = np.array([1, 2, 3, 4, 5])
y = np.array([2, 4, 5, 4, 5])
初始化参数
theta = np.array([0, 0])
学习率和迭代次数
alpha = 0.01
iterations = 1000
梯度下降
for i in range(iterations):
计算预测值
y_pred = X.dot(theta)
计算梯度
gradient = (1/len(X)) (X.T.dot(y_pred - y))
更新参数
theta -= alpha gradient
print(\"Optimized theta:\", theta)
```
2. 逻辑回归
逻辑回归常用于二分类问题。我们可以使用梯度下降来找到最佳分类边界。
```python
import numpy as np
假设的数据点
X = np.array([[1, 2], [2, 3], [3, 3], [4, 5], [5, 6]])
y = np.array([0, 0, 1, 1, 1])
将X转换为列向量
X_b = np.c_[np.ones((len(X), 1)), X] 添加偏置项
初始化参数
theta = np.random.randn(X_b.shape[1])
学习率和迭代次数
alpha = 0.1
iterations = 1500
梯度下降
for i in range(iterations):
逻辑回归的预测值
z = X_b.dot(theta)
h = 1 / (1 + np.exp(-z))
计算梯度
gradient = X_b.T.dot(h - y) / len(X)
更新参数
theta -= alpha gradient
print(\"Optimized theta:\", theta)
```
3. 神经网络
梯度下降是训练神经网络的关键算法,通常与反向传播结合使用。
```python
假设这是一个简单的神经网络,包含一个输入层、一个隐藏层和一个输出层
这里省略了网络的具体实现细节
初始化网络参数
...
学习率和迭代次数
alpha = 0.01
iterations = 10000
梯度下降
for i in range(iterations):
前向传播
...
计算损失
...
反向传播
...
计算梯度
...
更新网络参数
...
print(\"Optimized network parameters:\", params)
```
在实际应用中,我们通常会使用像scikit-learn、TensorFlow或PyTorch这样的库来简化梯度下降的实现,并利用它们提供的高级功能,如自动微分、优化器等。这些库提供了优化算法的高效实现,包括但不限于梯度下降及其变体(如随机梯度下降SGD、小批量梯度下降Mini-batch GD等)。
梯度下降算法是理解和实现许多机器学习算法的基础,是优化理论中的一个重要组成部分。