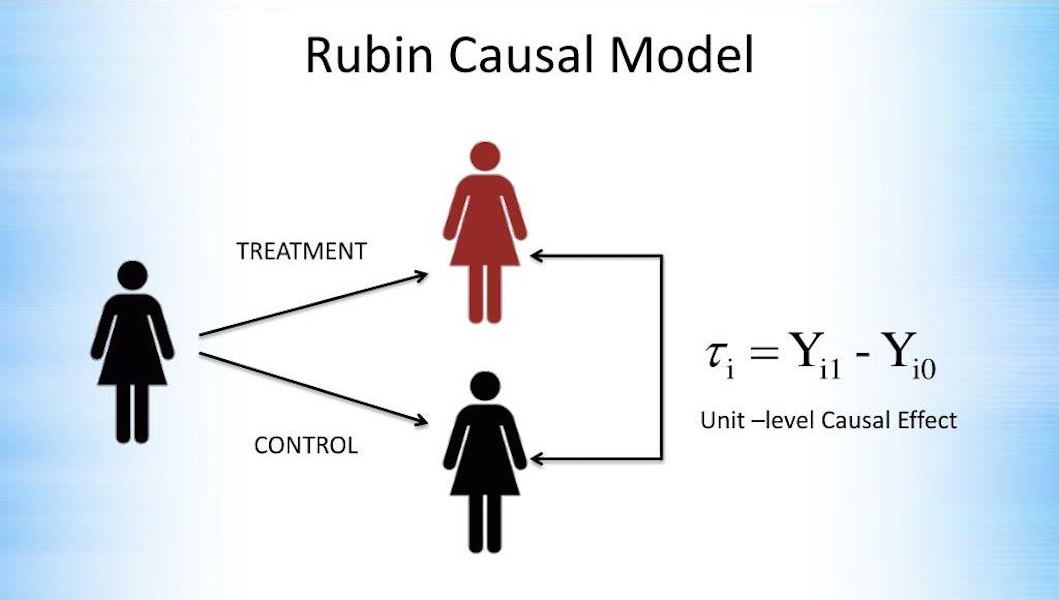
潜在结果模型(Rubin Causal Model,简称RCM),又称潜在结果框架(Potential Outcomes Framework),是现代因果推断领域最基础、核心的理论范式之一。该模型由统计学家内曼(Neyman)于1923年初步提出,后经唐纳德·鲁宾(Donald Rubin)在1974年、1978年的研究进一步发展和推广,正式确立了其在因果推断中的主导地位,还因在健康、社会科学等领域的重要应用,成为2021年诺贝尔经济学奖相关理论的核心基础。
一、核心思想与核心要素
RCM的核心思想的是通过**构想个体在所有可能处理状态下的潜在结果**,来严谨定义因果效应,本质是回答“反事实问题”——若个体处于不同处理状态(如接受治疗/不接受治疗、参与项目/不参与项目),结果会产生何种差异,这种差异即为因果效应。其核心要素包括以下三部分:
1.处理变量(Treatment Variable)
通常设为二分类变量,记为Zᵢ(或Tᵢ),用于区分个体的处理状态:Zᵢ=1表示个体i接受处理(如接种疫苗、参与扶贫项目),Zᵢ=0表示个体i处于对照状态(如接种安慰剂、未参与项目)。部分扩展模型可支持多水平处理变量。
2.潜在结果(Potential Outcomes)
对每个个体i,存在两个对应的潜在结果:Yᵢ(1)表示个体i接受处理(Zᵢ=1)时的结果,Yᵢ(0)表示个体i处于对照状态(Zᵢ=0)时的结果。现实中,我们仅能观察到个体实际所处状态的结果,即Yᵢ = Zᵢ·Yᵢ(1) + (1-Zᵢ)·Yᵢ(0),另一个未观察到的结果即为“反事实结果”,这是因果推断的核心痛点。
3.协变量(Covariates)
记为Xᵢ,是同时影响处理分配和结果的变量(如研究补习班效果时,学生的基础成绩、学习时间等)。协变量的合理控制是消除混杂偏差、准确推断因果效应的关键。
二、核心假设
由于反事实结果无法直接观测,RCM需依赖三个关键假设,才能从观测数据中识别和估计因果效应,其中部分假设可检验,部分为不可检验的结构性假设。
1.稳定单元处理值假设(SUTVA)
该假设包含两层含义:一是“无干扰”,即一个个体的处理状态不会影响其他个体的结果(如研究疫苗效果时,A接种疫苗不会影响B的感染风险);二是“处理唯一性”,即处理和对照状态仅有唯一明确的定义(如研究网课效果时,需统一网课形式,避免部分用直播、部分用录播的情况)。SUTVA是模型成立的基础,若违反会导致因果效应估计偏差。
2.可忽略性假设(Ignorability)
又称无混杂假设,核心是“给定协变量Xᵢ,处理分配与潜在结果独立”,数学表达为(Yᵢ(1), Yᵢ(0)) ⊥ Zᵢ | Xᵢ。其含义是:在控制所有相关协变量后,处理组和对照组个体的潜在结果无系统性差异,处理分配类似随机化。该假设不可直接检验,需通过理论分析和协变量充分性验证间接支撑(如确保无遗漏关键混杂变量)。
3.正值性假设(Positivity)
又称重叠性假设,指对所有协变量组合X=x,个体被分配到处理组和对照组的概率均介于0和1之间,数学表达为0 < P(Zᵢ=1 | Xᵢ=x) < 1。其核心是“每个协变量组合下,都有个体同时处于处理组和对照组”,确保能找到可比个体进行结果对比。该假设可检验,若存在某类协变量组合仅出现在处理组或对照组,会导致对应群体的因果效应无法识别。
三、因果效应的核心估计量
RCM定义了不同层面的因果效应估计量,以适配不同研究目标,核心包括三类:
1.个体处理效应(ITE)
针对单个个体i,因果效应为其两种潜在结果的差值:τᵢ = Yᵢ(1) - Yᵢ(0)。由于反事实结果缺失,ITE无法直接观测,仅能通过群体层面的平均效应推断。
2.总体平均处理效应(ATE)
指目标总体中所有个体处理效应的期望,数学表达为τ = E[Yᵢ(1) - Yᵢ(0)],反映处理对总体的平均影响,是最常用的核心估计量。
3.条件平均处理效应(CATE)
指给定协变量X=x的子群体的平均处理效应,数学表达为τ(x) = E[Yᵢ(1) - Yᵢ(0) | Xᵢ=x]。CATE可用于分析处理效应的异质性(如不同年龄、性别群体中,处理效果的差异)。
四、常见估计方法
在满足上述假设的前提下,常用以下方法从观测数据中估计因果效应,各方法适用于不同数据场景:
1.倾向得分加权(IPW)
基于可忽略性假设,通过倾向得分e(Xᵢ) = P(Zᵢ=1 | Xᵢ)对样本加权:处理组个体权重为1/e(Xᵢ),对照组个体权重为1/(1-e(Xᵢ)),加权后协变量在两组间达到平衡,再通过加权平均差估计ATE。
2.回归调整
构建结果回归模型(如线性回归、广义加性模型),将处理变量和协变量同时纳入模型,直接控制混杂变量的影响。例如通过模型Yᵢ = β₀ + β₁Zᵢ + β₂Xᵢ + εᵢ,系数β₁即为ATE的估计值(需假设模型设定正确)。
3.双重稳健估计(AIPW)
结合倾向得分加权和回归调整的优势,构建增强逆概率加权模型。其核心特点是“稳健性”——只要倾向得分模型或结果回归模型中有一个设定正确,即可得到无偏的ATE估计,降低单一模型误判导致的偏差风险。
五、应用场景与价值
RCM已成为医疗、社会科学、经济学、机器学习等领域因果推断的核心工具,解决了“关联≠因果”的经典困境,典型应用场景包括:
•医疗领域:评估新药疗效、疫苗保护力,排除患者基线特征等混杂因素的影响;
•社会科学:评估扶贫项目、教育政策的效果(如网课对成绩的影响、现金补贴对家庭收入的提升作用);
•机器学习:解决推荐系统、自动驾驶等场景的可解释性问题(如“若未推荐该商品,用户是否会购买”),推动模型从“关联预测”走向“因果决策”。
六、争议与扩展
RCM的核心争议集中在对“反事实逻辑”的依赖——部分学者(如统计学家Dawid)对其底层的条件排中律(CEM)提出质疑,认为并非所有反事实结果都存在明确定义。同时,为适配复杂场景,RCM不断扩展,如结合因果贝叶斯网络解决多变量因果链问题、引入动态处理模型适配时序数据,进一步提升了模型的适用性和灵活性。