一、算法概述
高斯-牛顿(Gauss-Newton, GN)算法是一种专为**非线性最小二乘问题**设计的迭代优化算法,是牛顿法在最小二乘问题场景下的改进变种。其核心目标是通过迭代调整模型参数,使模型预测值与实际观测数据之间的残差平方和最小化,广泛应用于数据拟合、参数估计等科学与工程领域。该算法由数学家卡尔·弗里德里希·高斯和艾萨克·牛顿命名,最早可追溯至高斯1809年的著作《天体运动论》中,后经完善形成现代常用形式。
与通用优化的牛顿法不同,GN算法针对最小二乘问题的特殊结构进行简化,无需显式计算复杂的Hessian矩阵(二阶导数矩阵),仅通过雅可比矩阵(一阶导数矩阵)近似二阶信息,在保证收敛效率的同时降低了计算复杂度。
二、核心原理
1.问题定义
设待优化的非线性最小二乘问题目标函数为残差平方和:
S(β) = Σ(i=1至m)[rᵢ(β)]²
其中,β = (β₁, β₂, …, βₙ)ᵀ 为n维待估计参数向量,rᵢ(β) = f(xᵢ, β) - yᵢ 为第i个观测值的残差(f(xᵢ, β)为模型预测值,yᵢ为实际观测值),m为观测数据量且满足m ≥ n(超定系统)。算法的核心是找到β*使S(β)最小。
2.核心简化思路
GN算法通过对残差函数rᵢ(β)进行一阶泰勒展开线性化,近似替代原非线性问题,进而转化为一系列线性最小二乘问题迭代求解。其关键简化在于对Hessian矩阵的近似:
原目标函数的Hessian矩阵H表达式为:
H = Σ(i=1至m)[∇rᵢ(β)·∇rᵢ(β)ᵀ + rᵢ(β)·∇²rᵢ(β)]
GN算法忽略残差的二阶导数项rᵢ(β)·∇²rᵢ(β),仅保留一阶导数构成的项,并用雅可比矩阵J近似Hessian矩阵:H ≈ JᵀJ。其中,雅可比矩阵J为m×n矩阵,元素定义为Jᵢⱼ = ∂rᵢ(β)/∂βⱼ,反映残差对各参数的敏感度。
3.迭代更新公式
基于上述近似,通过求解线性方程组(正规方程)得到参数更新增量δ,迭代更新参数:
β^(k+1) = β^(k) - (JₖᵀJₖ)⁻¹Jₖᵀrₖ
其中,β^(k)为第k次迭代的参数值,Jₖ为当前参数下的雅可比矩阵,rₖ为当前残差向量,(JₖᵀJₖ)⁻¹Jₖᵀ为伪逆矩阵(解决超定系统求解问题)。
三、迭代流程
GN算法的完整迭代步骤如下,流程清晰且易于工程实现:
1.初始化:给定参数初始猜测值β^(0),设置收敛阈值ε(用于判断迭代终止),迭代次数计数器k=0。
2.计算残差:代入当前参数β^(k),计算残差向量rₖ = (r₁(β^(k)), r₂(β^(k)), …, rₘ(β^(k)))ᵀ。
3.计算雅可比矩阵:通过解析求导或数值差分(如有限差分法)计算Jₖ,确保矩阵元素准确性。
4.构建并求解正规方程:计算JₖᵀJₖ和Jₖᵀrₖ,求解线性方程组JₖᵀJₖ·δ = -Jₖᵀrₖ得到增量δ。若JₖᵀJₖ奇异或病态,可采用QR分解、SVD分解或阻尼策略(如Levenberg-Marquardt算法的阻尼项)保证求解稳定性。
5.更新参数:β^(k+1) = β^(k) + δ,k = k + 1。
6.收敛判断:若参数增量的范数||δ|| < ε或残差平方和增量||S(β^(k+1)) - S(β^(k))|| < ε,则停止迭代,输出最优参数β^(k+1);否则返回步骤2继续迭代。
四、优缺点分析
1.优点
•计算效率高:无需计算复杂的Hessian矩阵,仅依赖雅可比矩阵运算,大幅降低高维问题的计算成本和内存占用,优于标准牛顿法。
•收敛速度快:相比梯度下降法,利用了二阶曲率信息(雅可比矩阵近似),在初始值接近真实解时收敛速率显著更快。
•针对性强:专为非线性最小二乘问题设计,适配数据拟合、参数估计等场景的核心需求,实用性强。
2.缺点
•初始值敏感:作为局部优化算法,收敛效果严重依赖初始参数β^(0)。若初始值偏离真实解过远,可能收敛到局部极小值或直接发散,需通过经验、分段法或线性化预处理确定合理初始值。
•矩阵奇异性风险:JᵀJ可能存在奇异或病态情况,导致增量δ无法求解,需结合数值稳定方法优化。
•线性化误差影响:忽略残差二阶项可能引入近似误差,在残差较大、模型高度非线性时,可能导致迭代震荡或收敛缓慢。
•适用范围有限:仅针对非线性最小二乘问题,无法直接处理通用无约束优化或约束优化问题。
五、与牛顿法的区别
GN算法作为牛顿法的变种,二者在核心逻辑、适用场景上存在显著差异,具体对比如下:
从适用问题来看,标准牛顿法适用于通用无约束优化问题,而高斯-牛顿法仅针对性解决非线性最小二乘问题,适用场景更聚焦。在Hessian矩阵处理上,标准牛顿法需要计算完整的二阶导数矩阵,运算复杂度高,而高斯-牛顿法无需二阶导数,仅通过雅可比矩阵J构造JᵀJ来近似Hessian矩阵,大幅简化计算。二者计算成本差异显著,标准牛顿法计算成本极高,在高维场景下耗时严重,高斯-牛顿法计算成本更低,仅依赖一阶导数运算即可完成迭代。收敛条件方面,标准牛顿法需满足目标函数凸性良好且初始值合适,才能实现二阶收敛;高斯-牛顿法的收敛效果则依赖残差线性化精度,仅能实现局部收敛。
六、典型应用场景
GN算法因在非线性最小二乘问题上的高效性,在多个领域具有广泛应用:
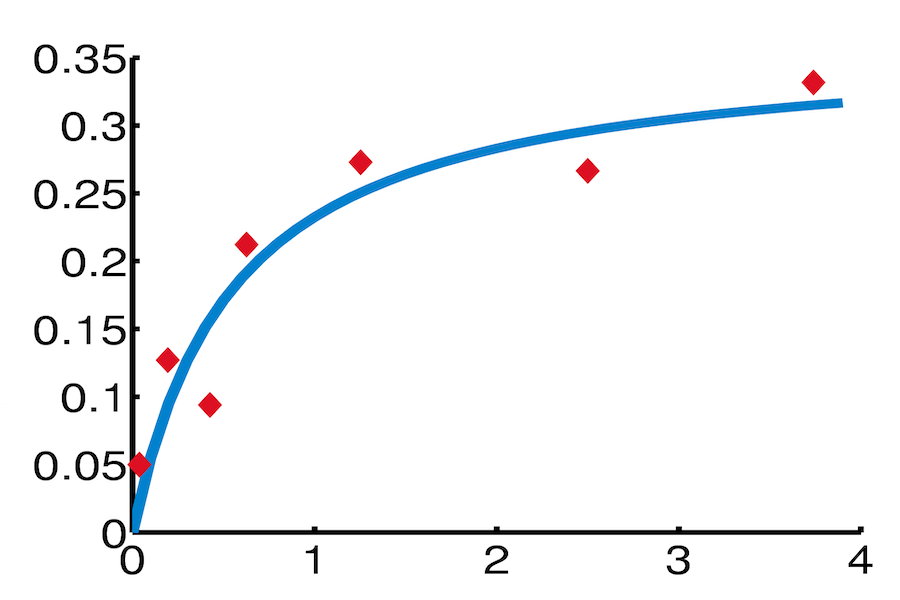
1.曲线拟合:对非线性模型(如指数衰减模型y = a·e^(bx)、Logistic模型)进行数据拟合,估计模型参数,常见于化学动力学、生物生长规律分析等场景。
2.计算机视觉:相机标定(估计内参焦距、畸变系数及外参位置姿态)、光束平差法(Bundle Adjustment)、三维重建(从二维图像估计三维点坐标)等核心任务。
3.机器人学:SLAM(同时定位与建图)系统中,通过传感器数据优化机器人位姿和环境地图参数,实现精准定位与地图构建。
4.控制系统:系统辨识,通过输入输出数据估计非线性系统的模型参数,为控制策略设计提供依据。
5.数据分析:非线性回归分析、实验数据校准,消除观测误差对参数估计的影响,提升模型可靠性。
七、改进与拓展
针对GN算法的缺陷,学界提出了多种改进方案,其中最具代表性的是Levenberg-Marquardt(LM)算法。LM算法通过引入阻尼项λI(λ为阻尼系数,I为单位矩阵),将正规方程修正为(JᵀJ + λI)·δ = -Jᵀr,可动态调节阻尼系数平衡GN算法的收敛速度与稳定性:λ较小时接近GN算法,λ较大时接近梯度下降法,有效解决初始值敏感和矩阵病态问题。