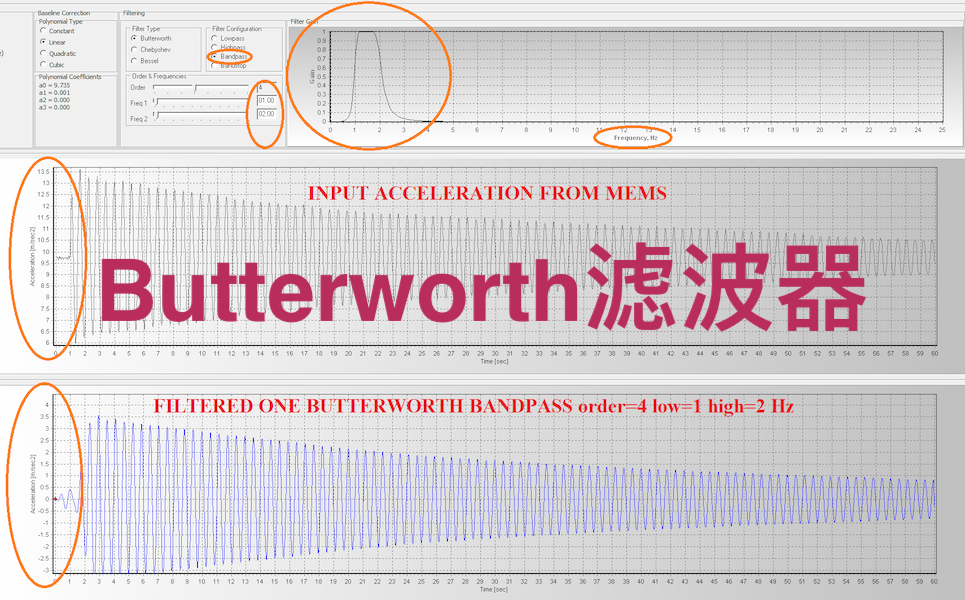
Butterworth滤波器,又称“最平幅度滤波器”,是由英国工程师Stephen Butterworth于1930年提出的一种线性相位滤波器。其核心特点是在通带内幅频特性具有最大平坦度,没有纹波,而在阻带内则呈现单调衰减的特性。这种特性使得它在对通带信号保真度要求较高的场景中得到广泛应用,相较于Chebyshev滤波器等其他类型,Butterworth滤波器的通带信号失真更小,不过其阻带衰减速度相对较慢,通常需要更高的阶数才能达到与其他滤波器相当的阻带抑制效果。
一、核心特性
1.幅频特性
Butterworth滤波器的幅频特性是其最显著的标志,具体表现为:
•通带平坦:在规定的通带频率范围内,幅度响应的波动极小,接近理想的平坦特性,这是其“最平”名称的由来。
•阻带单调衰减:随着频率超出通带范围,幅度会单调递减,没有纹波,衰减速度与滤波器的阶数正相关,阶数越高,阻带衰减越快,越接近理想滤波器的矩形幅频特性。
2.相位特性
Butterworth滤波器属于线性相位滤波器的一种,其相位响应与频率呈近似线性关系。这意味着不同频率的信号经过滤波器后,产生的相位延迟与频率成正比,能够有效避免信号的相位失真,保证输出信号的波形与输入信号的波形基本一致,仅存在时间上的延迟。
二、关键公式
1.幅频响应公式
Butterworth滤波器的幅频响应函数定义为输出信号幅度与输入信号幅度的比值,其通用表达式为:
|H(jω)| = 1 / √[1 + (ω/ω_c)^(2n)]
其中各参数含义如下:
•|H(jω)|:滤波器的幅度响应(无量纲);
•ω:输入信号的角频率(单位:rad/s),ω = 2πf,f为信号频率(单位:Hz);
•ω_c:滤波器的3dB截止角频率(单位:rad/s),对应的截止频率f_c = ω_c/(2π),此时|H(jω_c)| = 1/√2 ≈ 0.707,即信号幅度衰减3dB;
•n:滤波器的阶数(正整数),阶数越高,幅频特性越接近理想滤波器。
2.传递函数
Butterworth滤波器的复频率传递函数H(s)基于极点分布推导得出,其极点位于s平面的左半平面(保证滤波器稳定),且均匀分布在以ω_c为半径的半圆上。对于低通Butterworth滤波器,其传递函数的标准形式为:
H(s) = ω_c^n / [∏(k=1到n) (s - s_k)]
其中极点s_k的表达式为:
s_k = -ω_c · e^(jπ(2k + n - 1)/(2n)) ,k = 1, 2, ..., n
式中j为虚数单位(j² = -1),极点的实部均为负值,确保了滤波器的稳定性。
3.不同类型滤波器的频率变换
通过频率变换,可以由低通Butterworth滤波器推导出高通、带通和带阻滤波器,常见的变换公式如下:
1)低通→高通:令s' = ω_c / s,其中s'为高通滤波器的复频率变量,ω_c为低通滤波器的截止角频率,变换后高通滤波器的截止角频率与原低通滤波器一致。
2)低通→带通:令s' = ω_c(s² + ω_0²)/(s(ω_h - ω_l)),其中ω_0为带通滤波器的中心角频率(ω_0 = √(ω_lω_h)),ω_l和ω_h分别为带通滤波器的下、上截止角频率,ω_c为原低通滤波器的截止角频率。
3)低通→带阻:令s' = ω_c s(ω_h - ω_l)/(s² + ω_0²),参数含义与带通变换一致,实现对特定频率范围信号的抑制。
三、设计步骤
Butterworth滤波器的设计通常遵循“指标确定→阶数计算→极点求解→传递函数构建→电路实现”的流程,具体步骤如下:
1.明确设计指标
根据实际应用需求,确定滤波器的核心指标,主要包括:
•滤波器类型(低通、高通、带通、带阻);
•通带截止频率f_p(或通带频率范围)及通带最大衰减A_p(通常A_p ≤ 1dB);
•阻带截止频率f_s(或阻带频率范围)及阻带最小衰减A_s(通常A_s ≥ 20dB~60dB);
•采样频率f_samp(数字滤波器设计时需确定)。
2.计算滤波器阶数n
根据通带和阻带的衰减要求,利用幅频响应公式推导阶数n的计算式:
n ≥ log₁₀[(10^(A_s/10) - 1)/(10^(A_p/10) - 1)] / [2log₁₀(ω_s/ω_p)]
其中ω_p为通带角频率,ω_s为阻带角频率,计算得出的n需取大于等于该值的最小正整数。
3.确定3dB截止角频率ω_c
将n代入通带或阻带的衰减条件,求解ω_c,通常取满足通带衰减要求的ω_c值:
ω_c = ω_p / (10^(A_p/10) - 1)^(1/(2n))
4.求解传递函数并实现
根据ω_c和n计算极点s_k,构建传递函数H(s)。对于模拟滤波器,可通过RC、LC电路或运算放大器实现;对于数字滤波器,需通过脉冲响应不变法、双线性变换法等将模拟传递函数转换为数字传递函数,再通过编程(如MATLAB、Python)或专用芯片实现。
四、应用场景
Butterworth滤波器因其通带平坦、相位线性的特性,在多个领域得到广泛应用,典型场景包括:
1.信号预处理:在传感器信号采集(如温度、压力传感器)中,用于滤除高频噪声,保留低频有用信号,确保信号的准确性。
2.通信系统:用于信号的频带限制,如在基带传输中抑制码间串扰,或在射频电路中滤除杂波干扰,提升通信质量。
3.音频处理:在音响、录音设备中,用于音频信号的均衡调节,如低通滤波保留低音成分,高通滤波增强高音细节,且因通带平坦不会导致音频失真。
4.生物医学工程:在心电图(ECG)、脑电图(EEG)等生物电信号处理中,滤除工频干扰(50Hz/60Hz)和高频噪声,突出生物电信号的特征波形。
5.图像处理:用于图像的平滑去噪(低通滤波)或边缘提取(高通滤波),改善图像质量或为后续图像分析提供支持。
五、优缺点
1.优点
•通带幅频特性平坦,无纹波,信号失真小,适合对信号保真度要求高的场景;
•相位响应近似线性,可避免信号相位失真;
•设计方法成熟,公式推导清晰,易于通过软件或硬件实现。
2. 缺点
•阻带衰减速度较慢,达到相同阻带抑制效果时,所需阶数高于Chebyshev滤波器等,导致电路复杂度或计算量增加;
•在对阻带衰减速度要求极高的场景中,性价比相对较低。