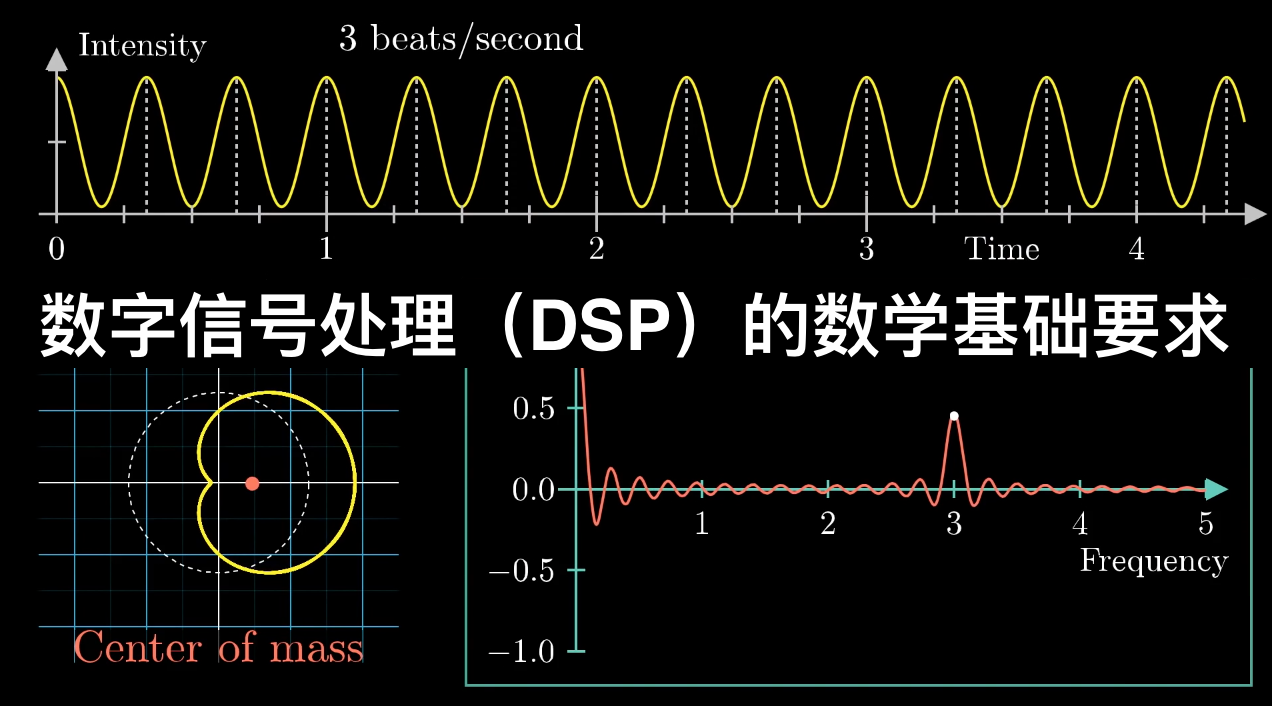
数字信号处理(DSP)是康复医疗设备信号处理的核心理论支撑,其入门阶段的数学基础聚焦“实用工程数学”——无需深入纯数学推导,重点掌握“概念理解+应用层面的计算/工具使用”,核心围绕“离散信号的描述、变换、分析”展开。结合康复医疗场景(IMU步态数据、EEG脑电信号、EMG肌电信号处理),以下是分层次的数学基础要求:
一、必备基础
1.高等数学(微积分核心内容)
核心知识点
•导数与微分:理解“变化率”(如IMU加速度信号是速度的导数,速度是位移的导数)。
•定积分与不定积分:掌握积分的物理意义(“面积求和”,如EMG信号的积分(AUC)反映肌肉收缩总量)。
•级数(重点是傅里叶级数):理解“周期信号可分解为不同频率的正弦/余弦波叠加”(这是频域分析的核心思想)。
•极限与连续性:理解离散信号的收敛性(如滤波算法中数据的稳定性)。
康复场景应用
•积分:计算IMU加速度信号的积分,得到步态的位移(步长估算);计算EMG信号的积分,评估康复训练中肌肉的总收缩量。
•傅里叶级数:将周期性的EEG信号(如alpha波8-13Hz)分解为不同频率成分,提取特定频段的能量(BCI康复设备的核心逻辑)。
学习要求
•无需掌握复杂积分推导(如多重积分),重点理解“物理意义”和“工程应用”。
•会用工具计算(如Python的numpy.integrate、小程序JS的简单求和积分)。
2.线性代数(矩阵与向量基础)
核心知识点
•向量与矩阵:信号的表示(如多通道EEG数据可表示为“时间×通道”的矩阵,单通道信号是一维向量)。
•矩阵运算:加法、乘法、转置(多通道信号的合并、特征提取中的数据变换)。
•行列式与逆矩阵(基础概念):了解即可,入门阶段极少直接使用。
•特征值与特征向量(入门级理解):知道“特征向量是信号的核心成分”(如PCA降维用于EEG数据去噪)。
康复场景应用
•矩阵表示:3通道IMU数据(加速度X/Y/Z)可表示为[x1,x2,...,xn; y1,y2,...,yn; z1,z2,...,zn]的矩阵,方便批量处理(如滤波、标准化)。
•向量运算:计算信号的均值向量(IMU零漂校准:减去各轴均值)、方差向量(评估信号稳定性)。
学习要求
•掌握基础矩阵/向量运算规则(无需深入线性空间、秩等抽象概念)。
•理解“信号=向量/矩阵”的映射关系,能用电线工具(如numpy矩阵运算、JS数组模拟向量)实现计算。
3.复变函数(重点是复数运算)
核心知识点
•复数的定义与运算:实部、虚部、模、辐角,复数的加减乘除、共轭(傅里叶变换的基础)。
•欧拉公式:e^(jθ) = cosθ + j sinθ(连接复数与三角函数,是频域分析的关键桥梁)。
•复变函数的基础概念(如解析函数):了解即可,入门阶段无需深入。
康复场景应用
•傅里叶变换:将时域的实信号(如EEG、IMU数据)转换为频域的复信号,通过复数的模(幅值谱)获取信号的频率成分强度,辐角(相位谱)反映频率成分的时间同步性。
•滤波算法:IIR滤波器的设计中,复数用于表示极点和零点,决定滤波特性(但入门阶段可通过工具直接调用滤波器,无需手动设计)。
学习要求
•核心掌握“复数运算”和“欧拉公式”,能理解“频域复信号的物理意义”(无需推导复变函数的积分、留数等高深内容)。
•知道“模=信号幅值,辐角=相位”即可,不用纠结数学本质。
4.概率论与数理统计(统计特征分析)
核心知识点
•随机变量与概率分布:理解信号的随机性(如噪声是随机变量,服从正态分布)。
•数字特征:均值、方差、标准差、协方差(信号预处理和特征提取的核心)。
•概率密度函数(PDF):了解即可,入门阶段重点用数字特征描述信号。
康复场景应用
•均值:IMU零漂校准(静止时采集3秒数据,计算各轴均值,后续数据减去该均值);EEG信号基线校正(减去全时段均值,去除基线漂移)。
•方差/标准差:评估信号的稳定性(如康复训练中EMG信号的标准差增大,可能表示肌肉发力不稳定)。
•协方差:分析多通道EEG信号的相关性(如判断不同脑区的活动同步性)。
学习要求
•无需掌握复杂的概率分布推导(如泊松分布、伽马分布),重点掌握“均值、方差、协方差”的计算与应用。
•会用工具计算(如Python的numpy.mean、numpy.var,小程序JS的数组求和计算均值)。
5.离散数学(离散序列与递推关系)
核心知识点
•离散序列:数字信号的本质(连续信号采样后得到的离散点序列,如IMU 100Hz采样率即100个点/秒的离散序列)。
•递推关系:差分方程(如IIR滤波器的实现:y[n] = a1*y[n-1] + a2*y[n-2] + b1*x[n] + b2*x[n-1])。
•集合与逻辑:了解即可,用于理解信号的“子集”(如特定频段的信号)。
康复场景应用
•离散序列操作:滑动窗口滤波(如3点滑动均值:y[n] = (x[n-2]+x[n-1]+x[n])/3),用于IMU数据平滑。
•递推关系:小程序端实时实现IIR低通滤波(通过递推公式避免复杂计算,降低延迟)。
学习要求
•掌握“离散序列的索引、递推公式的理解与实现”(重点是代码层面的应用,如JS中的for循环实现递推)。
•无需深入离散数学的抽象理论(如格、图论)。
二、进阶补充
这类知识在入门阶段(如IMU步态处理、基础EEG滤波)可暂时跳过,当需要处理更复杂的信号(如非平稳EEG信号、多模态数据融合)时再补充:
1.傅里叶变换与拉普拉斯变换(核心是离散傅里叶变换DFT)
核心知识点
•离散傅里叶变换(DFT):将离散时域信号转换为频域信号(入门阶段重点是“应用”,而非推导)。
•快速傅里叶变换(FFT):DFT的高效算法(实际开发中用工具调用,如numpy.fft.fft)。
•拉普拉斯变换:用于分析线性系统的稳定性(如滤波器设计),入门阶段了解即可。
康复场景应用
•DFT/FFT:对EEG信号进行频域分析,提取alpha波(8-13Hz)、beta波(14-30Hz)的能量占比,作为BCI康复设备的控制指令(如alpha波能量高于阈值时启动康复机器人)。
•频谱分析:通过FFT查看IMU信号的频率成分,确定滤波的截止频率(如去除50Hz工频噪声)。
学习要求
•入门阶段无需掌握DFT的数学推导,重点理解“时域→频域”的转换意义(时域看信号随时间变化,频域看信号的频率成分)。
•会用工具实现FFT(如Python的numpy.fft、小程序的dsp.js中FFT函数),能解读频谱图(横轴是频率,纵轴是幅值)。
2.线性系统理论
核心知识点
•线性、时不变(LTI)系统:信号处理中大多数滤波器都是LTI系统(满足“叠加性”和“时不变性”)。
•卷积与相关:卷积是线性系统的核心运算(如FIR滤波器的实现本质是信号与滤波器系数的卷积)。
•冲激响应与频率响应:了解“冲激响应决定系统特性”,频率响应反映系统对不同频率信号的衰减/放大作用。
康复场景应用
•卷积:FIR低通滤波(如IMU数据的5Hz低通滤波,通过信号与滤波系数的卷积实现平滑)。
•频率响应:设计陷波滤波器(50Hz),其频率响应在50Hz处幅值衰减,其他频率幅值不变,用于去除EEG/EMG信号的工频噪声。
学习要求
•入门阶段理解“卷积=滑动加权求和”,能通过工具实现(如numpy.convolve),无需手动计算卷积积分。
•知道LTI系统的基本性质(叠加性、时不变性),能判断滤波器是否符合要求。
3.优化理论
核心知识点
•目标函数与约束条件:如滤波器设计中“最小化噪声功率”作为目标函数。
•梯度下降:简单理解即可,用于后续机器学习辅助信号分类(如EEG动作想象分类)。
康复场景应用
•滤波器参数优化:如通过梯度下降调整IIR滤波器的系数,使滤波后的信号信噪比(SNR)最高。
•特征提取优化:如优化EMG信号的特征组合(峰值、方差、积分),使假肢控制的准确率最高。
学习要求
•入门阶段无需掌握复杂的优化算法推导,重点了解“优化的核心是找到最优参数”,能使用现成的优化工具(如scipy.optimize)。
三、无需深入的数学内容
入门阶段无需纠结以下内容,重点聚焦“实用操作”:
•纯数学推导:如傅里叶变换的严格证明、复变函数的留数定理、线性代数的Jordan标准型等。
•高深分支:如泛函分析、实变函数、偏微分方程(仅在高阶DSP应用中涉及,如小波变换的深入研究)。
•复杂概率模型:如贝叶斯网络、马尔可夫链(入门阶段用简单的统计特征即可满足需求)。
四、康复医疗场景下的数学基础学习建议
1.学习顺序:先应用后理解,先工具后理论
第一步:掌握“必备基础”中的核心操作(如均值、方差计算,复数的模运算,离散序列的递推),先用工具(Python/JS)实现简单的信号处理(如IMU数据零漂校准、滑动窗口滤波)。
第二步:结合实际场景反推数学原理(如用FFT处理EEG数据后,再回头理解傅里叶变换的“时域转频域”意义)。
第三步:按需补充“进阶内容”(如需要设计自定义滤波器时,再学习线性系统理论;需要做信号分类时,再补充优化理论)。
2.重点聚焦“工程应用”,而非“数学推导”
•例如:无需手动计算DFT, but 要知道“FFT能得到信号的频率成分”,会用numpy.fft.fft计算,能解读频谱图(如EEG信号在8-13Hz有峰值,说明alpha波活跃)。
•例如:无需推导卷积公式, but 要知道“卷积能实现滤波”,会用numpy.convolve实现FIR滤波,能调整滤波系数改变平滑效果。
3.结合康复场景强化记忆
•每个数学知识点都绑定具体应用(如“均值→IMU零漂校准”“FFT→EEG频域特征提取”“卷积→FIR滤波”),避免孤立学习数学。
•用实际数据验证(如采集IMU数据,计算均值后减去,观察数据是否平稳;对EEG数据做FFT,观察50Hz工频噪声的幅值)。
4.工具辅助降低数学门槛
•用Python的numpy(矩阵/向量运算)、scipy(积分、FFT、滤波)、matplotlib(可视化数学结果)简化计算。
•用小程序的dsp.js(封装了FFT、滤波算法)、math.js(复数运算、矩阵运算),无需手动实现复杂数学逻辑。
五、总结
数字信号处理入门的数学基础核心是“实用工程数学”,聚焦“微积分(导数/积分)、线性代数(矩阵/向量)、复变函数(复数运算)、概率论(均值/方差)、离散数学(离散序列)”五大模块,无需深入纯数学推导。对于康复医疗开发者而言,学习的关键是“将数学知识点与IMU、EEG、EMG等信号处理场景绑定”,通过工具实现实操,再反推理论理解,最终支撑“硬件采集→软件处理→康复应用”的技术闭环。
入门阶段的数学基础足够支撑以下应用:
•IMU步态数据的预处理(零漂校准、滤波、步长/步频计算)。
•EEG/EMG信号的去噪(工频陷波、高低通滤波)、频域特征提取。
•小程序端实时信号处理(滑动窗口、简单统计特征计算)。
当需要开展更复杂的应用(如自定义滤波器设计、BCI信号分类算法)时,再补充线性系统理论、优化理论等进阶内容即可。