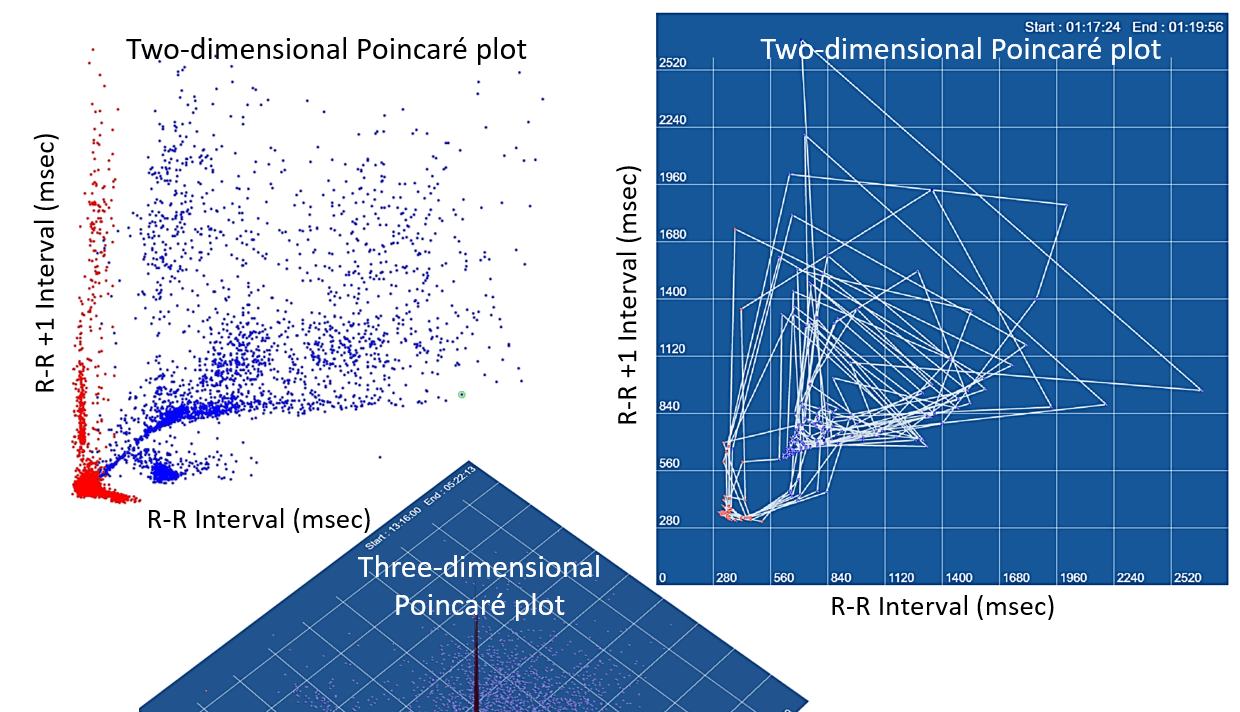
Poincaré Plot(庞加莱图),又称洛伦兹图(Lorenz Plot),是由法国数学家亨利·庞加莱(J.H.Poincaré)提出的一种非线性动力学分析工具,核心用于将一维时间序列数据转化为二维散点图,从而直观揭示系统的动态行为模式、稳定性及混沌特性。作为混沌理论的核心分析方法之一,它被广泛应用于生物医学、气候科学、天文学等多个领域,尤其在心率变异性(HRV)分析中已成为临床常用技术。
一、核心定义与作图原理
庞加莱图的本质是通过“迭代映射”将时间序列的动态特征可视化,其核心逻辑是构建相邻数据点的二维对应关系,具体作图步骤如下:
1.数据提取:获取目标系统的一维时间序列数据,如心电信号中的RR间期(两次R波之间的时间间隔)、气象数据中的气温序列等。
2.迭代配对:以序列中第n个数据点作为横坐标(X=RRₙ),第n+1个相邻数据点作为纵坐标(Y=RRₙ₊₁),形成散点(RRₙ, RRₙ₊₁);依次迭代配对所有数据点,如(RR₁, RR₂)、(RR₂, RR₃)……(RRₙ, RRₙ₊₁)。
3.图形绘制:将所有配对形成的散点绘制于二维直角坐标系中,最终形成的散点集合即为庞加莱图。通过散点的分布形态、密度及结构,可反推原始时间序列的动力学特性。
这种作图方式具有迭代计算的独特性质,能将抽象的时间序列转化为具象的几何图形,使复杂系统的内在规律更易观察。
二、核心概念:吸引子与庞加莱截面
庞加莱图的分析核心依赖“吸引子”与“庞加莱截面”两大概念,二者共同构成了对非线性系统行为的解读框架:
1.吸引子
吸引子是描述动力学系统在相空间(虚拟的数学空间,用于表征系统所有可能状态)中终极行为模式的几何构形,具有稳定、吸引的特性,能反映系统演化的最终趋势。根据系统类型,吸引子可分为两类:
•平庸吸引子:对应周期系统,相空间维数为整数,结构简单、边缘规则。例如人工机械起搏器固定频率起搏的RR序列,其庞加莱图散点分布规则,呈现明显的周期性特征。
•奇怪吸引子:对应非线性混沌系统,具有分数维结构,形态复杂、轮廓不规则,是混沌系统无序稳态的直观体现。例如正常人窦性心律的RR序列,其庞加莱图呈“棒球拍”形,内部散点分布紊乱但整体轮廓稳定,具有分形自相似性。
吸引子的核心特性的是不可分割性,不同动力系统无法融合为同一吸引子,因此通过吸引子形态可快速区分系统类型及行为模式。
2.庞加莱截面
非线性系统的吸引子多为高维复杂立体结构(如洛伦兹吸引子的“蝴蝶状”立体构形),难以直接观察。庞加莱提出通过“截面剖切”的方式,将高维吸引子转化为二维图形,即庞加莱截面——相当于对高维吸引子做“切片”处理,所得截面的散点分布可精准反映原吸引子的内部结构。
1960年代,洛伦兹借助计算机绘制出气象系统的奇怪吸引子及庞加莱截面,揭示了气象系统的混沌特性,进一步推动了庞加莱图在非线性系统分析中的应用。
三、庞加莱图的核心特征与分析方法
庞加莱图的分析分为定性与定量两类,核心基于散点的形态、密度及衍生指标判断系统特性:
1.定性特征
•分形性:混沌系统的庞加莱图具有自相似性,同一数据不同时段的图形形态一致,仅细节存在差异。
•确定性与随机性统一:混沌系统的散点轮廓具有稳定性(确定性),但内部散点位置随机,与出现顺序无关。
•分岔现象:系统可在周期与混沌状态间转换,体现为庞加莱图形态的突变,反映系统动力学特性的改变。
2.定量指标
为精准量化系统特性,常通过椭圆拟合等方法提取指标,其中最常用的是:
•短轴标准差(SD1):反映系统短期波动性,对应椭圆短轴长度,体现相邻数据点的变异程度。
•长轴标准差(SD2):反映系统长期波动性,对应椭圆长轴长度,体现整体序列的变异趋势。
•SD1/SD2比值:用于区分系统混沌程度,不同生理病理状态下该比值存在显著差异,是临床诊断的重要依据。
四、主要应用领域
庞加莱图因能直观解析非线性系统特性,在多个领域具有广泛应用,其中生物医学领域最为成熟:
1.生物医学(核心应用领域)
在心率变异性分析中,庞加莱图可通过RR序列散点形态判断心脏状态:
•正常人窦性心律呈“棒球拍”形奇怪吸引子,SD1/SD2比值稳定;
•心衰患者呈平庸吸引子,图形结构简单、面积大;
•房性早搏、室性早搏等心律失常具有特征性散点分布,可实现快速分型诊断。
此外,还可用于分析呼吸模式、脑电信号等生理序列,辅助神经系统疾病、呼吸系统疾病的诊断。
2.气候与气象科学
用于分析气温、降水、气压等时间序列,通过庞加莱图的吸引子形态揭示气候系统的混沌特性,为长期气候预测提供理论支撑,如洛伦兹吸引子对气象混沌系统的表征。
3.其他领域
•天文学:研究行星运动轨迹的稳定性,通过庞加莱截面分析天体系统的动态演化。
•流体力学:探索湍流、涡旋等复杂流体行为,揭示流体系统的非线性动力学规律。
•经济学:分析金融市场价格序列,判断市场波动的混沌特性与稳定性。
五、局限性与发展趋势
1.局限性
传统二维庞加莱图存在时序信息丢失、高维系统表征不足的问题,难以全面反映复杂系统的动态演化过程;同时,散点图分析易受噪声干扰,对数据质量要求较高。
2.发展趋势
为突破二维局限,三维庞加莱图分析方法应运而生,通过引入第三个维度(如RRₙ₊₂)保留更多时序信息,结合局部分布熵等指标实现更精准的量化分析。此外,结合符号动力学、机器学习等技术,可进一步提升庞加莱图在疾病诊断、系统预测中的准确率,拓展其应用场景。
综上,庞加莱图作为非线性系统分析的经典工具,以其直观性、实用性在多学科领域发挥重要作用,随着技术迭代,其对复杂系统的解析能力将持续提升。