在信号处理、控制系统、自动驾驶等众多领域,我们常常需要从包含噪声的观测数据中提取出系统真实的状态信息。卡尔曼滤波(Kalman Filter)作为一种高效的递归滤波算法,凭借其对线性系统的最优估计能力,成为解决这类问题的经典工具。
一、卡尔曼滤波的基本概念
卡尔曼滤波由鲁道夫·卡尔曼(Rudolf E. Kalman)于1960年提出,其本质是一种基于线性系统状态方程和观测方程,利用递推方式对系统状态进行最优估计的算法。与传统的批处理滤波(如最小二乘法)不同,卡尔曼滤波不需要存储全部历史观测数据,而是通过当前观测值和上一时刻的状态估计值,实时计算出当前的最优状态估计,具有计算量小、实时性强的显著优势。
核心特点:
•递归性:仅依赖上一时刻的状态估计结果和当前观测值,无需历史数据回溯。
•最优性:在观测噪声和系统噪声均为高斯白噪声的假设下,能够给出系统状态的最小均方误差(MMSE)估计。
•线性假设:基础卡尔曼滤波仅适用于线性系统,针对非线性系统需扩展为扩展卡尔曼滤波(EKF)或无迹卡尔曼滤波(UKF)等。
二、卡尔曼滤波的核心思想
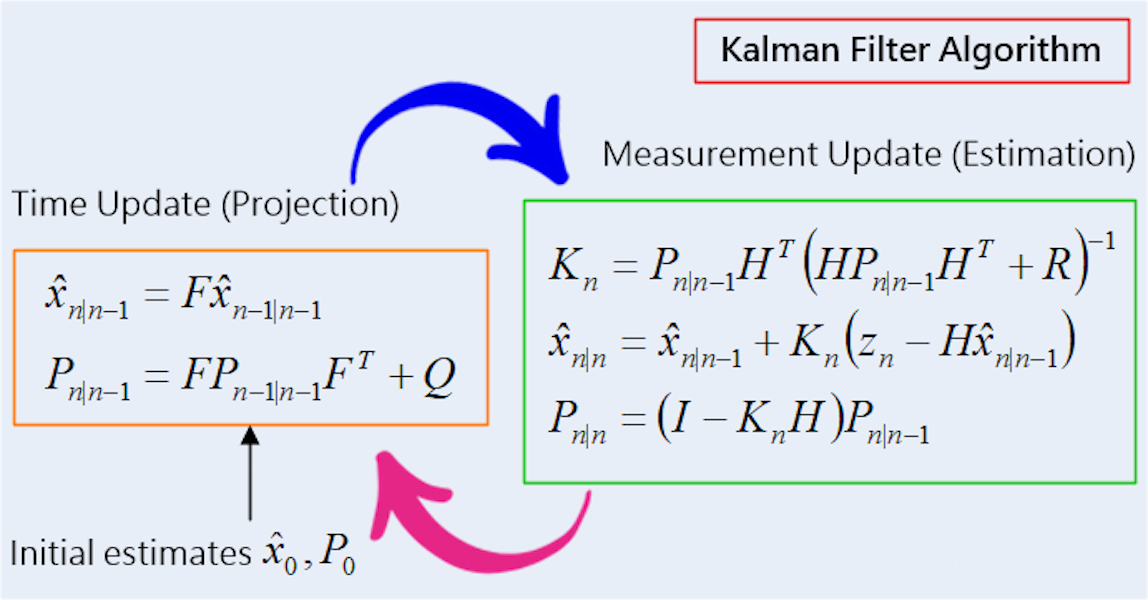
卡尔曼滤波的核心思想可以概括为“预测-更新”两个循环迭代的步骤,通过不断修正对系统状态的估计,逐步逼近真实状态。
1.预测步骤(Predict):根据系统的运动模型(状态方程),利用上一时刻的最优状态估计值,预测当前时刻的系统状态估计值(称为“先验估计”),同时预测出当前状态估计的误差协方差矩阵,反映先验估计的不确定性。
2.更新步骤(Update):结合当前时刻的观测数据,计算“观测残差”(观测值与基于先验估计的预测观测值之差),然后根据系统噪声和观测噪声的统计特性,计算“卡尔曼增益”(用于权衡先验估计和观测数据的可靠性),最终利用卡尔曼增益和观测残差,对先验估计进行修正,得到当前时刻的最优状态估计(称为“后验估计”),并更新状态估计的误差协方差矩阵。
简单来说,卡尔曼滤波就是通过“预测”给出一个初步的状态估计,再通过“更新”利用观测数据对这个初步估计进行修正,使得修正后的估计更接近系统的真实状态,并且这个过程会随着时间的推移不断重复。
三、卡尔曼滤波的数学模型
要应用卡尔曼滤波,首先需要建立系统的状态方程和观测方程,这是卡尔曼滤波的数学基础。假设系统为线性时不变系统,且噪声为高斯白噪声,其数学模型如下:
1.状态方程
状态方程描述了系统状态随时间的演化规律,形式为:
x(k) = A · x(k-1) + B · u(k) + w(k)
各参数含义:
•x(k):k时刻系统的状态向量(待估计的量,如位置、速度等);
•x(k-1):k-1时刻系统的状态向量;
•A:状态转移矩阵,描述k-1时刻状态到k时刻状态的线性变换关系;
•B:控制输入矩阵,描述控制输入对系统状态的影响;
•u(k):k时刻的控制输入向量(若系统无控制输入,可令B=0或u(k)=0);
•w(k):k时刻的系统过程噪声向量,服从高斯分布,即w(k) ~ N(0, Q),其中Q为过程噪声的协方差矩阵。
2.观测方程
观测方程描述了观测数据与系统状态之间的线性关系,形式为:
z(k) = H · x(k) + v(k)
各参数含义:
•z(k):k时刻的观测向量(如传感器测量值);
•H:观测矩阵,描述系统状态到观测值的线性变换关系;
•v(k):k时刻的观测噪声向量,服从高斯分布,即v(k) ~ N(0, R),其中R为观测噪声的协方差矩阵;
•过程噪声w(k)和观测噪声v(k)相互独立。
四、卡尔曼滤波的核心公式(工作流程)
卡尔曼滤波的工作过程就是“预测-更新”的循环,每个循环包含5个核心公式,具体步骤如下:
1.初始化(Initialization)
在滤波开始前,需要对初始状态和初始误差协方差矩阵进行估计:
•初始状态估计:x̂(0|0) = E[x(0)](通常根据先验知识或经验设定);
•初始误差协方差矩阵:P(0|0) = E[(x(0) - x̂(0|0))(x(0) - x̂(0|0))ᵀ](若对初始状态不确定,可设为较大的对角矩阵)。
2.预测步骤(Predict)
根据状态方程,预测k时刻的先验状态和先验误差协方差:
1)先验状态估计:x̂(k|k-1) = A · x̂(k-1|k-1) + B · u(k) 该公式表示利用k-1时刻的最优状态估计,结合系统的状态转移和控制输入,预测k时刻的系统状态。
2)先验误差协方差矩阵:P(k|k-1) = A · P(k-1|k-1) · Aᵀ + Q 该公式表示先验估计的误差由两部分组成:一是k-1时刻最优估计的误差通过状态转移后的传播,二是k时刻系统过程噪声带来的误差。
3)更新步骤(Update)
结合k时刻的观测值,对先验估计进行修正,得到k时刻的后验最优估计:
3.计算卡尔曼增益(Kalman Gain):K(k) = P(k|k-1) · Hᵀ · (H · P(k|k-1) · Hᵀ + R)⁻¹ 卡尔曼增益是卡尔曼滤波的核心参数,其作用是权衡先验估计和观测数据的可靠性。若观测噪声较小(R小),则卡尔曼增益较大,说明更信任观测数据;若过程噪声较小(Q小),则卡尔曼增益较小,说明更信任先验估计。
4.后验状态估计(最优估计):x̂(k|k) = x̂(k|k-1) + K(k) · (z(k) - H · x̂(k|k-1)) 其中z(k) - H · x̂(k|k-1)为观测残差,代表观测值与先验预测观测值之间的差异。该公式通过卡尔曼增益对先验估计进行修正,得到更接近真实状态的后验估计。
5.后验误差协方差矩阵:P(k|k) = (I - K(k) · H) · P(k|k-1) 其中I为单位矩阵。该公式更新了后验估计的误差协方差,反映了k时刻最优估计的不确定性,将作为下一时刻预测步骤的输入。
完成k时刻的更新后,系统将进入k+1时刻的“预测-更新”循环,如此往复,实现对系统状态的实时最优估计。
五、卡尔曼滤波的关键假设与局限性
1.关键假设
基础卡尔曼滤波的最优性依赖于以下两个核心假设:
•系统线性:系统的状态演化和观测过程均满足线性关系,即状态方程和观测方程为线性方程。
•噪声高斯性:过程噪声w(k)和观测噪声v(k)均为零均值高斯白噪声,且两者相互独立。
2.局限性
当实际系统不满足上述假设时,基础卡尔曼滤波的性能会显著下降,其局限性主要体现在:
•无法直接处理非线性系统,对于非线性系统,需采用扩展卡尔曼滤波(EKF,通过泰勒展开将非线性系统线性化)、无迹卡尔曼滤波(UKF,通过采样点近似高斯分布)等改进算法。
•对噪声协方差矩阵Q和R的设置较为敏感,若Q和R的估计不准确,会导致滤波发散或估计精度降低。实际应用中,常通过自适应卡尔曼滤波等方法动态调整Q和R。
六、卡尔曼滤波的典型应用场景
由于其高效的实时最优估计能力,卡尔曼滤波在众多领域得到了广泛应用,典型场景包括:
1.导航与定位:在GPS导航、惯性导航系统(INS)中,卡尔曼滤波可融合GPS的观测数据和惯性传感器的测量数据,解决GPS信号遮挡时的定位问题,提高定位精度和稳定性。例如,自动驾驶车辆的定位系统常采用卡尔曼滤波及其改进算法。
2.目标跟踪:在雷达、红外、视觉跟踪系统中,卡尔曼滤波可根据目标的历史运动状态(如位置、速度)预测其当前位置,并结合传感器的观测数据,实现对目标的稳定跟踪,克服观测噪声带来的干扰。
3.信号处理:在通信系统中,卡尔曼滤波可用于去除信号传输过程中的噪声,恢复原始信号;在语音处理中,可用于语音增强,降低背景噪声。
4.控制系统:在工业控制、机器人控制等领域,卡尔曼滤波可估计系统的不可直接观测状态(如电机的转速、负载扭矩),为控制器提供准确的状态反馈,提高控制系统的性能。
5.传感器数据融合:当系统存在多个不同类型的传感器(如温度传感器、湿度传感器、压力传感器)时,卡尔曼滤波可融合各传感器的观测数据,得到比单一传感器更准确、更可靠的状态估计。
七、总结
卡尔曼滤波作为一种经典的线性系统最优估计算法,以“预测-更新”的递归结构为核心,在高斯白噪声环境下能够给出系统状态的最小均方误差估计,具有计算量小、实时性强的优势。尽管基础卡尔曼滤波依赖于线性和高斯噪声假设,但通过扩展卡尔曼滤波、无迹卡尔曼滤波等改进算法,其应用范围已扩展到非线性系统领域。