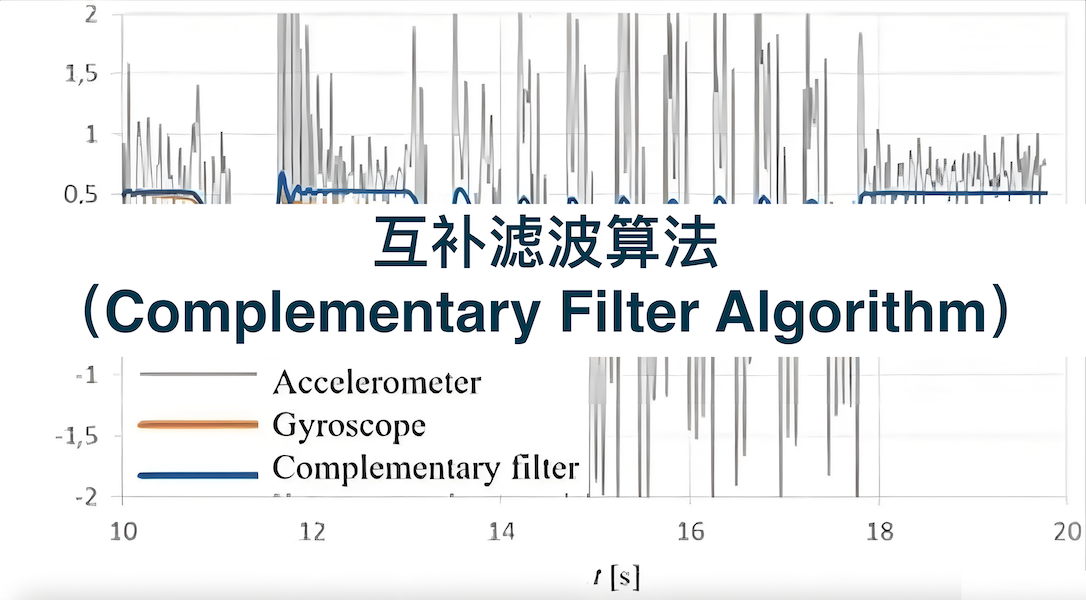
在传感器数据融合领域,互补滤波算法以其结构简单、计算量小、实时性强的特点,成为低成本惯性导航、姿态解算等场景的核心技术之一。它通过利用不同传感器的“互补特性”——即一种传感器在高频段精度高、低频段误差大,另一种传感器则相反——实现对目标状态的精准估计,有效弥补单一传感器的性能缺陷。
一、核心概念:什么是互补滤波?
互补滤波是一种线性滤波方法,其核心思想是“频率互补”:针对同一物理量(如角度、速度、位置),将两个或多个具有互补频率特性的传感器数据进行融合,使融合后的输出在全频率范围内都保持较高精度。
最典型的应用场景是“惯性传感器+外部参考传感器”的组合:
•惯性传感器(如陀螺仪):能快速响应物理量的变化,高频段测量精度高,但存在零点漂移,误差会随时间累积(低频段误差大);
•外部参考传感器(如加速度计、磁力计、GPS):测量结果稳定,低频段精度高,但响应速度慢,易受高频噪声干扰(高频段误差大)。
互补滤波通过滤波策略让两种传感器“各司其职”:用惯性传感器的数据跟踪高频变化,用参考传感器的数据修正低频漂移,最终输出兼顾快速响应与长期稳定的融合结果。
二、核心原理:频率分割与误差修正
互补滤波的本质是通过低通滤波器(LPF)和高通滤波器(HPF)对不同传感器数据进行频率分割,再将分割后的有效成分叠加,实现误差抵消。其原理可从“频率域”和“时域”两个维度理解:
1. 频率域原理
设两个传感器对同一物理量的测量输出分别为S₁(t)(如陀螺仪输出,高频优、低频差)和S₂(t)(如加速度计输出,低频优、高频差),融合后的输出为O(t)。
互补滤波的频率特性满足:
•对S₁(t)施加高通滤波(HPF,High-Pass Filter),保留高频成分:HPF(S₁(t))
•对S₂(t)施加低通滤波(LPF,Low-Pass Filter),保留低频成分:LPF(S₂(t))
•融合输出:O(t) = HPF(S₁(t)) + LPF(S₂(t))
理想状态下,高通滤波器(HPF)与低通滤波器(LPF)的频率响应满足“互补条件”:HPF(f) + LPF(f) = 1(对所有频率f),确保全频率范围内的信号都被有效覆盖,无信息丢失或重复叠加。
2. 时域原理(递推修正)
在实际工程应用中,为满足实时性要求,互补滤波更多以“递推修正”的时域形式实现。以姿态解算中“陀螺仪+加速度计”的组合为例,其核心逻辑是:
1.预测步骤:用陀螺仪的角速度数据积分,得到当前姿态的预测值(跟踪高频变化);
2.修正步骤:用加速度计计算得到姿态的参考值(反映低频稳定状态),与预测值对比得到误差;
3.融合步骤:通过滤波系数将误差反馈到预测值中,修正漂移,得到最终姿态输出。
这种“预测-修正”的逻辑,本质是将高频的动态响应与低频的稳定参考相结合,实现误差的实时补偿。
三、数学模型与实现公式
互补滤波的数学模型可分为“连续时间模型”和“离散时间模型”,其中离散模型是工程实现的核心。以下以最常用的“一阶互补滤波”为例,介绍其核心公式。
1. 一阶互补滤波(First-Order Complementary Filter,离散形式)
设离散时间序列为k(k=0,1,2,...),采样周期为T,滤波系数为α(0 < α < 1),则融合输出的递推公式为:
O(k) = α·O_pred(k) + (1 - α)·S₂(k)
其中:
•O_pred(k):第k时刻的预测值(如陀螺仪积分得到的姿态),对应高通滤波(HPF)后的成分;
•S₂(k):第k时刻的参考传感器输出(如加速度计计算的姿态),对应低通滤波(LPF)后的成分;
•α:滤波系数,决定两种传感器数据的权重——α越大,预测值(高频成分)权重越高,响应速度越快,但抗漂移能力越弱;α越小,参考值(低频成分)权重越高,稳定性越强,但响应速度越慢。
进一步地,预测值O_pred(k)通常由上一时刻的融合输出与惯性传感器数据计算得到,以姿态解算(角度θ)为例:
O_pred(k) = O(k-1) + ω(k)·T
其中ω(k)为陀螺仪在第k时刻的角速度输出,T为采样周期。将其代入融合公式,可得完整的递推模型:
O(k) = α·[O(k-1) + ω(k)·T] + (1 - α)·S₂(k)
2. 滤波系数α的物理意义(First-Order Complementary Filter)
一阶互补滤波(First-Order Complementary Filter)的频率特性由系数α和采样周期T共同决定,其截止频率f_c(高通与低通的分界频率)可通过下式计算:
f_c = (1 - α) / (2π·α·T)
截止频率的含义是:低于f_c的信号主要由参考传感器(S₂)主导,高于f_c的信号主要由惯性传感器(S₁)主导。因此,α的调整本质是调整频率分割的边界,以适配不同传感器的特性。
四、关键参数设计与优化
互补滤波的性能高度依赖参数设计,核心是滤波系数α的选取。不合理的参数会导致融合结果“响应滞后”或“漂移严重”,需结合传感器特性和应用场景优化。
1. 固定系数α的选取方法
对于静态或慢动态场景(如机器人平稳行走、手机姿态检测),可通过“经验法”或“频域分析法”确定固定系数:
•经验法:先将α设为0.98~0.99(优先保留高频成分),若发现输出漂移严重,减小α(如0.95);若发现响应滞后,增大α(如0.995),反复调试至平衡。
•频域分析法:通过传感器标定,确定惯性传感器的漂移频率(如陀螺仪漂移主要集中在0.1Hz以下)和参考传感器的噪声频率(如加速度计噪声集中在10Hz以上),将截止频率\\( f_c \\)设为两者之间(如1Hz),再通过公式反推α。
2. 自适应系数优化(Adaptive Complementary Filter)
对于动态变化剧烈的场景(如无人机机动飞行、汽车急加速),固定系数难以兼顾“动态响应”与“稳定性”,需采用自适应互补滤波——根据传感器误差或系统动态特性实时调整α:
•基于误差反馈的自适应:计算预测值与参考值的误差e(k) = O_pred(k) - S₂(k),若误差较大(说明系统动态变化剧烈,参考传感器可能滞后),增大α;若误差较小(系统稳定,漂移占主导),减小α。
•基于传感器噪声的自适应:通过实时估计两种传感器的噪声方差(如用卡尔曼滤波中的噪声估计方法),动态调整α,使噪声方差小的传感器获得更高权重。
五、典型应用场景
互补滤波因低成本、高实时性的优势,被广泛应用于需要“动态响应+长期稳定”的场景,尤其在消费电子、机器人、无人机等领域。
1. 姿态解算(核心应用,Attitude Calculation with Complementary Filter)
在无人机、平衡车、智能手表中,需实时获取设备的姿态(俯仰角、横滚角、航向角)。通过“陀螺仪+加速度计+磁力计”的组合,互补滤波实现:
•陀螺仪积分得到姿态动态变化,跟踪高频动作(如无人机翻转);
•加速度计通过重力分量计算俯仰/横滚角,修正低频漂移;
•磁力计通过地磁场计算航向角,修正航向漂移。
相比复杂的卡尔曼滤波(Kalman Filter),互补滤波算法在姿态解算中可将计算量降低80%以上,同时满足100Hz以上的实时性要求。
2. 位置与速度估计
在室内定位或GPS信号弱的场景,通过“加速度计+GPS”的组合,互补滤波实现:
•加速度计积分得到速度和位置的高频变化(如行人步行动作);
•GPS提供低频稳定的位置参考,修正加速度计的积分漂移。
3. 工业过程控制
在温度、压力等过程控制中,将“快速响应传感器(如热电偶)”与“稳定参考传感器(如红外测温仪)”融合,互补滤波可消除高频干扰和低频漂移,实现精准控制。
六、优势与局限
1. 核心优势
•结构简单:无需复杂的矩阵运算或状态方程建模,工程实现难度低;
•计算量小:仅涉及基础的加减乘除运算,可在单片机等低端硬件上运行;
•实时性强:单步运算时间通常在微秒级,满足高频采样需求;
•鲁棒性好:对传感器噪声的适应性强,无需精确的噪声统计模型。
2. 主要局限
•线性假设限制:仅适用于线性系统,对强非线性场景(如无人机高速机动)适配性差;
•系数依赖经验:固定系数难以适配全动态范围,自适应优化需额外算法支持;
•多传感器融合能力弱:仅适用于两种互补传感器的融合,难以扩展到多传感器系统。
互补滤波算法是传感器数据融合领域的“轻量级方案”,其核心价值在于用最简单的逻辑实现“高频响应与低频稳定”的平衡。它不是卡尔曼滤波(Kalman Filter)等复杂算法的替代品,而是在低成本、高实时性场景下的最优选择之一。
随着技术发展,互补滤波已从“一阶固定系数”向“高阶自适应”“与卡尔曼滤波结合”等方向延伸(如“互补滤波+扩展卡尔曼滤波(EKF)”,兼顾简单性与高精度)。在实际应用中,需根据传感器特性、系统动态要求和硬件性能,选择合适的滤波结构与参数,才能最大化其性能优势。
随着技术发展,互补滤波已从“一阶固定系数”向“高阶自适应”“与卡尔曼滤波结合”等方向延伸(如“互补滤波+扩展卡尔曼滤波”,兼顾简单性与高精度)。在实际应用中,需根据传感器特性、系统动态要求和硬件性能,选择合适的滤波结构与参数,才能最大化其性能优势。