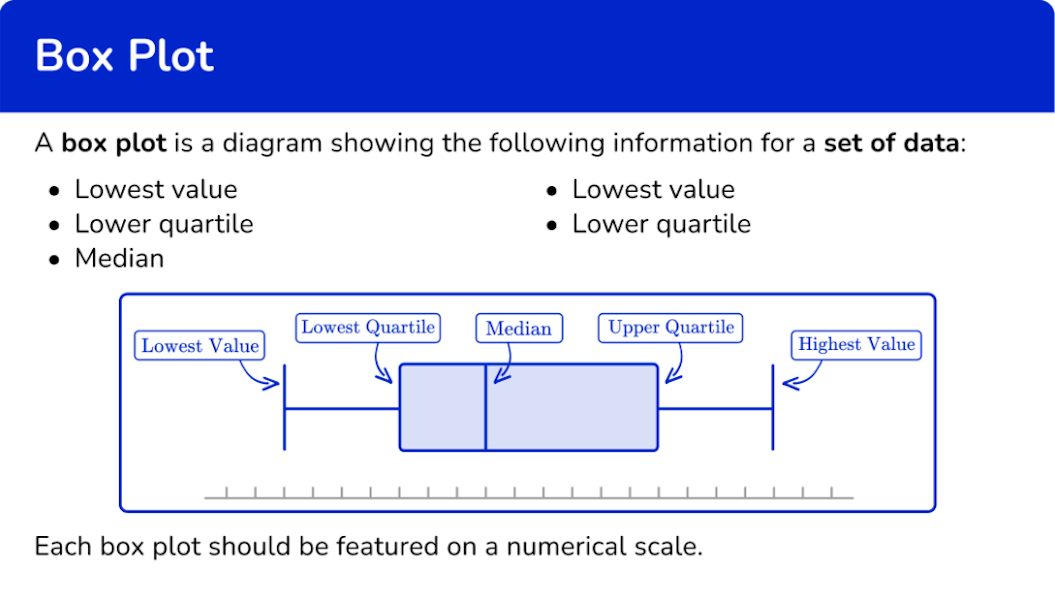
箱型图法则是数据处理领域中用于识别异常值(outliers)的经典统计方法,其核心逻辑基于数据的四分位数(quartile)分布特征,通过量化数据的离散程度来界定正常数据与异常值的边界,具有客观、高效且易操作的特点,被广泛应用于数据分析、质量控制、金融风控等多个领域。
一、关键统计指标
箱型图法则的应用首先需明确两个关键统计指标——四分位数,即下四分位数(First Quartile, Q1)和上四分位数(Third Quartile, Q3)。在有序排列的数据集中,Q1代表处于25%分位的数据值,意味着有25%的数据小于该值;Q3则代表处于75%分位的数据值,即有75%的数据小于该值。通过这两个分位数,可进一步计算出反映数据中间50%核心分布范围的指标——四分位距(Interquartile Range, IQR),其计算公式为IQR = Q3 - Q1。IQR的值越大,说明数据中间50%的分布越分散,反之则越集中。
异常值的判定是箱型图法则的核心环节。基于四分位距的特性,该法则设定了明确的异常值判定标准:当某一数据点的数值小于Q1 - 1.5IQR,或大于Q3 + 1.5IQR时,该数据点即被判定为异常值。这一判定边界的设定,既能够有效捕捉到显著偏离数据整体分布的极端值,又能最大程度避免将正常的随机波动数据误判为异常,实现了异常值识别的精准性与鲁棒性的平衡。
箱型图法则的价值不仅体现在理论层面,更在实际场景中展现出强大的应用能力,以下将结合两个典型案例具体说明。
二、案例一:电商平台日销售额异常值识别
某电商平台收集了30天的日销售额数据(单位:万元),为精准分析销售趋势,需先通过箱型图法则识别异常值。首先对30天数据按从小到大排序,计算得出Q1=52、Q3=88,由此可得IQR=88-52=36。根据判定标准,异常值边界为Q1-1.5IQR=52-1.5×36=2,Q3+1.5IQR=88+1.5×36=142。
梳理数据后发现,有两天数据超出边界:一天因系统故障导致销售额仅1万元(小于2万元),另一天因大型促销活动销售额达150万元(大于142万元)。这两个数据点均被判定为异常值。考虑到数据的连续性需求,平台未直接删除异常值,而是采用线性插值法补全。对于1万元的异常值,其前后相邻有效数据为3万元(第5天)和5万元(第7天),按公式计算补全值为4万元;对于150万元的异常值,前后有效数据为90万元(第22天)和85万元(第24天),补全值为87.5万元。补全后的数据更贴合日常销售趋势,为后续的库存规划、营销方案制定提供了可靠依据。
三、案例二:工业产品尺寸质量检测
某机械加工厂生产一批零件,需对其直径尺寸(单位:mm)进行质量检测,抽取50个零件的尺寸数据后,运用箱型图法则筛选异常值。经计算,数据的Q1=19.8、Q3=20.2,IQR=20.2-19.8=0.4,异常值边界为19.8-1.5×0.4=19.2,20.2+1.5×0.4=20.8。
检测发现有3个零件尺寸异常,分别为19.0mm、21.0mm、19.1mm,这些异常值可能是由机床精度波动、测量误差等原因导致。由于零件尺寸数据对生产调整至关重要,工厂采用线性插值法对异常值进行修正。以19.0mm的异常值为例,其前后合格零件尺寸为19.7mm(第18个)和19.9mm(第20个),计算得补全值为19.8mm。修正后的尺寸数据准确反映了零件生产的整体状态,帮助技术人员及时调整机床参数,降低了后续生产的不合格率。
四、案例三:智能鞋垫运动数据异常值处理
智能硬件公司研发的运动鞋垫,可实时采集用户跑步时的足底压力数据(单位:kPa),用于分析运动姿态与运动损伤风险。某用户连续佩戴鞋垫跑步30分钟,系统每1秒采集1组数据,共获得1800组压力数据,需通过箱型图法则处理数据中的异常值。
首先对1800组数据进行排序与统计,计算得出足底压力数据的Q1=125kPa、Q3=210kPa,因此四分位距IQR=210-125=85kPa。根据箱型图法则的异常值判定标准,计算得到异常值边界:下限为Q1-1.5IQR=125-1.5×85=0.5kPa,上限为Q3+1.5IQR=210+1.5×85=337.5kPa。
数据筛选后发现两类异常值:一类是压力值为0kPa的12组数据(小于0.5kPa),经排查为鞋垫与手机蓝牙短暂断连导致的数据缺失;另一类是压力值达350kPa的8组数据(大于337.5kPa),源于用户跑步时偶然踩入小坑导致的瞬时压力突变。由于这些异常值会干扰运动姿态分析的准确性,且数据具有明显的时间序列特征,采用线性插值法进行补全。
以第150秒的异常值(0kPa)为例,其前后相邻的有效数据为第149秒的130kPa和第151秒的135kPa,代入线性插值公式计算补全值:y=130 + (150-149)×(135-130)/(151-149)=132.5kPa。对于第220秒的350kPa异常值,前后有效数据为第219秒的205kPa和第221秒的212kPa,补全值为208.5kPa。补全后的压力数据完整呈现了用户跑步过程中足底压力的变化曲线,为后续的落地姿态优化建议提供了精准的数据支撑。
从上述案例可见,箱型图法则通过“四分位数定义范围—四分位距量化离散度—边界阈值判定异常”的完整逻辑链条,为异常值识别提供了标准化方案。同时,结合科学的异常值处理方法,既能剔除数据“噪声”,又能保证数据完整性,是数据预处理环节中不可或缺的重要工具。
五、常用开源函数库及基础应用
在实际数据处理中,无需手动编写复杂计算逻辑,主流编程语言的开源函数库已封装好箱型图法则的核心功能,以下为两类常用库的介绍及基础使用示例。
1.Python 生态:Pandas 与 Matplotlib/Seaborn
Python 作为数据分析主流语言,Pandas 库提供了四分位数计算与异常值筛选的便捷接口,Matplotlib 或 Seaborn 可用于可视化箱型图直观呈现异常值。
基础使用步骤:首先通过 Pandas 读取数据并计算四分位数与四分位距,然后依据箱型图法则判定异常值,最后结合 Matplotlib 绘制箱型图。示例代码逻辑如下:
import pandas as pd
import matplotlib.pyplot as plt
# 构造示例数据(模拟电商日销售额)
data = pd.Series([52, 60, 75, 88, 1, 150, 68, 72, 80])
# 计算四分位数
Q1 = data.quantile(0.25)
Q3 = data.quantile(0.75)
IQR = Q3 - Q1
# 定义异常值边界
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR
# 筛选异常值
outliers = data[(data < lower_bound) | (data > upper_bound)]
print(\"异常值:\", outliers.values)
# 绘制箱型图(直观展示异常值)
plt.boxplot(data, vert=False, patch_artist=True)
plt.xlabel(\"日销售额(万元)\")
plt.title(\"电商平台日销售额箱型图(含异常值标记)\")
plt.show()
上述代码中,Pandas 的 quantile() 方法可快速计算四分位数,通过简单逻辑即可筛选异常值,Matplotlib 的 boxplot() 函数会自动在图中标记出异常值(以圆点形式呈现)。
2.R 语言生态:dplyr 与 ggplot2
R 语言在统计分析领域应用广泛,dplyr 库可高效处理数据计算,ggplot2 库则擅长绘制专业的箱型图。
基础使用示例:利用 dplyr 计算统计量,结合 ggplot2 可视化异常值,代码逻辑如下:
library(dplyr)
library(ggplot2)
# 构造示例数据
data <- data.frame(销售额 = c(52, 60, 75, 88, 1, 150, 68, 72, 80))
# 计算四分位数与异常值边界
stats <- data %>%
summarize(Q1 = quantile(销售额, 0.25),
Q3 = quantile(销售额, 0.75),
IQR = Q3 - Q1,
lower_bound = Q1 - 1.5 * IQR,
upper_bound = Q3 + 1.5 * IQR)
# 筛选异常值
outliers <- data %>%
filter(销售额 < stats$lower_bound | 销售额 > stats$upper_bound)
print(outliers)
# 绘制箱型图
ggplot(data, aes(y = 销售额)) +
geom_boxplot(fill = \"lightblue\") +
labs(y = \"日销售额(万元)\", title = \"电商平台日销售额箱型图\") +
theme_minimal()
这些开源函数库的优势在于将箱型图法则的底层逻辑封装,使用者无需关注复杂的计算细节,只需调用相关接口即可快速完成异常值的识别与可视化,极大提升了数据处理效率。无论是Python还是R语言的库,都支持结合线性插值等方法进行异常值补全,可根据实际使用的编程语言生态灵活选择。