在数据驱动的时代,如何从海量数据中精准识别“不合群”的异常值,是数据分析、质量控制、科学实验等领域的核心需求之一。3σ准则,作为基于正态分布特性的经典异常值判定方法,以其简洁性和实用性,成为数据处理中的“基础工具”。它如同为数据装上了一台灵敏的“探测器”,能快速定位那些偏离数据整体规律的特殊值,为后续的决策与分析扫清障碍。
一、核心定义:从正态分布中诞生的判定标准
3σ准则的核心逻辑建立在数据的正态分布特性之上,其官方定义明确:对于服从正态分布N(μ,σ²)的数据集,当某个数据值x与数据集的均值μ之间的偏差绝对值超过3倍标准差σ,即满足|x - μ| > 3σ时,该数据值x将被判定为异常值。
这里需要明确三个关键参数的含义:一是数据值x,即待判定的单个数据点;二是均值μ,反映数据集的中心趋势,是所有数据的平均水平;三是标准差σ,衡量数据围绕均值的离散程度,σ越大说明数据分布越分散,σ越小则数据越集中。这三个参数共同构成了3σ准则的判定基石,缺一不可。
二、理论根基:正态分布的“3σ区间”特性
3σ准则并非凭空设定,其合理性完全源于正态分布的概率分布规律。正态分布,又称高斯分布,是自然界和社会经济领域中最常见的分布形态之一,如身高、体重、测量误差、产品尺寸等数据往往都近似服从正态分布。其概率密度曲线呈对称的“钟形”,数据主要集中在均值附近,越往两端数据出现的概率越低。
根据正态分布的概率积分计算,数据落在不同区间内的概率具有严格的固定值:
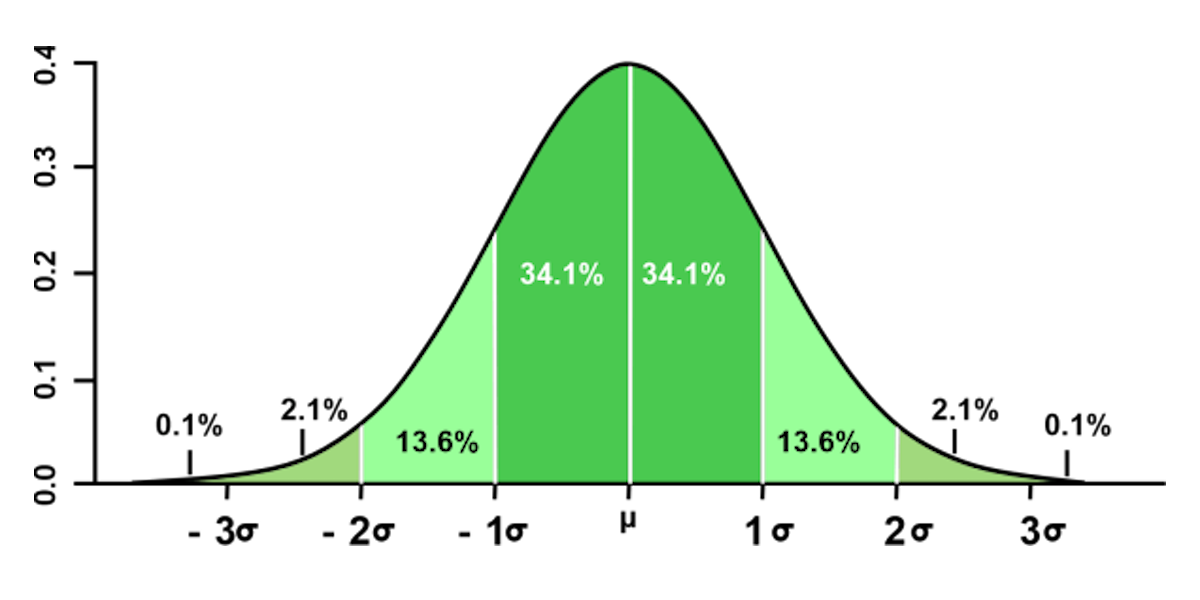
数据落在[μ - σ, μ + σ]区间内的概率约为68.27%,意味着超过三分之二的数据会集中在均值±1σ的范围内;
数据落在[μ - 2σ, μ + 2σ]区间内的概率约为95.45%,近九成五的数据会被包含在均值±2σ的区间内;
而数据落在[μ - 3σ, μ + 3σ]区间内的概率高达99.73%,几乎所有正常数据都会集中在这个区间内。
这就意味着,在正态分布的数据集里,数据值超出均值±3σ范围的概率仅为0.27%,属于极低概率事件。在统计学中,这种“小概率事件在一次试验中几乎不可能发生”的思想,正是3σ准则判定异常值的核心理论依据——当某个数据点落在这个极低概率区间时,我们有充分理由认为它并非来自正常的数据生成过程,而是异常值。
三、操作步骤:简单清晰的异常值识别流程
3σ准则的优势不仅在于理论扎实,更在于其操作步骤简洁明了,无需复杂的数学模型,普通数据分析者即可快速掌握。完整的操作流程主要包括以下四步:
第一步:确认数据分布形态
由于3σ准则是专为正态分布数据设计的方法,因此在使用前必须先验证数据集是否近似服从正态分布。常用的验证方法包括图形法和统计检验法:图形法可通过绘制直方图、Q-Q图(分位数-分位数图)直观判断,若直方图呈钟形对称分布、Q-Q图中数据点近似落在直线上,则说明数据近似正态;统计检验法可采用K-S检验(柯尔莫哥洛夫-斯米尔诺夫检验)、夏皮罗-威尔克检验等,通过计算检验统计量和P值来判断数据是否符合正态分布。
第二步:计算核心统计量μ和σ
对于已确认近似正态分布的数据集,计算其均值μ和标准差σ。均值μ的计算方法为所有数据值的总和除以数据个数;标准差σ的计算则需先求出每个数据值与均值的偏差平方和,再除以数据个数(总体标准差)或数据个数减一(样本标准差),最后取平方根。在实际应用中,可通过Excel的AVERAGE函数、STDEV函数,或Python的numpy库、R语言的mean函数和sd函数等工具快速计算。
第三步:确定异常值判定阈值
根据计算得到的μ和σ,确定异常值的判定区间:下限为μ - 3σ,上限为μ + 3σ。这个区间就是正常数据的“合理范围”,超出该范围的数值即为候选异常值。
第四步:逐一校验并标记异常值
将数据集中的每个数据值x与上述阈值进行比较,若满足|x - μ| > 3σ,则标记该数据值为异常值;若满足|x - μ| ≤ 3σ,则判定为正常数据。完成所有数据的校验后,可输出异常值的具体数值、位置及数量,为后续的处理提供依据。
四、应用场景与注意事项
凭借简洁性和高实用性,3σ准则在多个领域都有着广泛的应用,其中最典型的场景包括工业质量控制和数据预处理。在工业生产中,企业常利用3σ准则监控产品的关键尺寸、性能等指标,如汽车零部件的直径、电子元件的电阻值等,当检测数据超出μ ± 3σ范围时,立即触发质量警报,及时排查生产设备故障或原材料问题,这也是“六西格玛管理”的核心思想源头之一。在数据预处理环节,无论是机器学习建模还是数据分析报告撰写,都需要先通过3σ准则剔除异常值,避免异常值对模型训练(如线性回归模型对异常值敏感)或分析结果(如均值被异常值拉高或拉低)产生干扰。
但在使用3σ准则时,也需要注意其局限性:首先,仅适用于正态分布数据,若数据呈偏态分布、均匀分布等其他形态,使用3σ准则可能导致异常值识别不准确,此时应选用箱线图法、DBSCAN聚类法等更通用的异常值检测方法;其次,对小样本数据敏感性较高,小样本数据的均值和标准差计算结果稳定性较差,可能导致判定阈值出现偏差,因此3σ准则更适合大样本数据集;最后,异常值需结合业务场景二次确认,统计学上的异常值不一定是“错误值”,可能是实际业务中的特殊情况(如某电商平台“双十一”的销售额远超日常),需结合具体业务逻辑判断是否需要剔除或保留。
五、总结
3σ准则以正态分布的概率特性为核心,用“均值±3σ”这一简单阈值构建了高效的异常值识别体系,既具备扎实的统计学理论支撑,又拥有简洁易用的操作优势,成为数据分析领域的经典方法。在实际应用中,我们需牢记其适用条件,结合数据分布形态和业务场景灵活使用,让这一“异常值探测器”充分发挥作用,为数据质量保驾护航。