在数字时代的加密体系中,椭圆曲线加密技术(Elliptic Curve Cryptography,简称ECC)是继RSA之后最具影响力的非对称加密算法。它基于椭圆曲线的数学特性构建安全机制,凭借“短密钥、高安全、高效率”的优势,成为移动支付、物联网、区块链等场景的核心加密技术。
一、什么是椭圆曲线加密技术?
椭圆曲线加密技术是1985年由数学家Neal Koblitz和Victor Miller分别提出的非对称加密算法。其核心逻辑是:利用“椭圆曲线上的离散对数问题”的计算困难性,实现加密与解密的不对称性。
与RSA(基于大整数分解难题)相比,ECC的本质差异在于“安全基础的数学问题”:
RSA依赖“大整数分解为两个质数”的困难性,随着整数增大,破解难度呈多项式增长;
ECC依赖“椭圆曲线上找一个点的离散对数”的困难性,破解难度呈指数级增长,因此相同安全级别下,ECC的密钥更短。
二、核心原理:椭圆曲线与离散对数
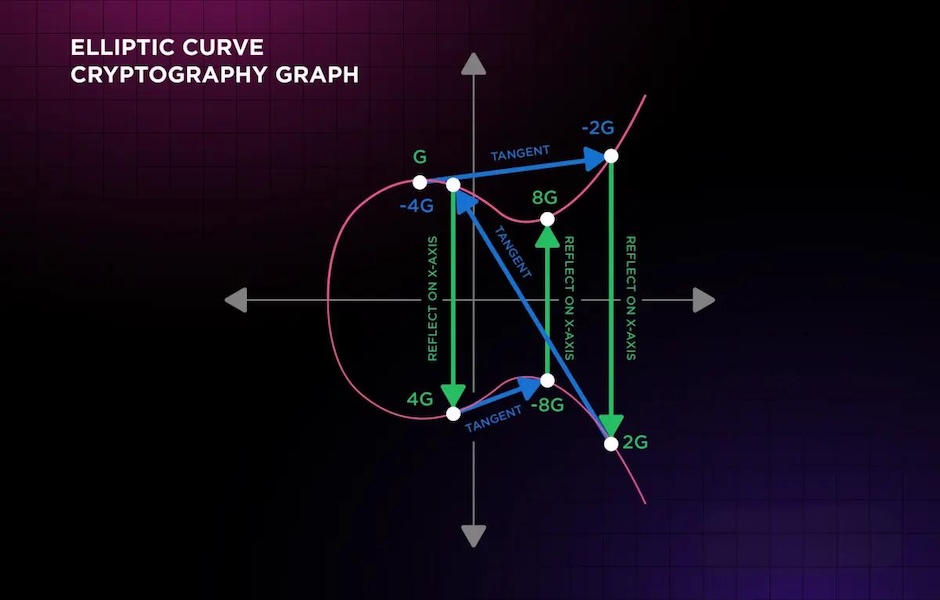
理解ECC无需深入复杂的数学证明,关键在于把握两个核心概念:椭圆曲线的定义、点运算规则。
1.椭圆曲线的定义
ECC使用的椭圆曲线并非实数域上的连续曲线,而是有限域(仅包含有限个整数点)上的离散曲线,其标准方程为:
y² ≡ x³ + ax + b (mod p)
其中,a、b是有限域内的常数(需满足4a³ + 27b² ≠ 0 mod p,避免曲线退化),p是一个大质数,“mod p”表示所有运算结果都限定在0到p-1的范围内。
这种“有限域”特性让曲线的点数量有限,为后续的加密运算提供了离散的、可控制的基础。
2.核心运算:点加与倍点
ECC的加密逻辑围绕“点运算”展开,最关键的是“点加”和“倍点”两种操作:
点加:给定椭圆曲线上的两个不同点P和Q,通过特定规则(连接P、Q的直线与曲线的第三个交点,再关于x轴对称)得到新点R,记为R = P + Q;
倍点:点加的特殊情况,即P和Q为同一点,此时直线为P点的切线,与曲线的另一个交点对称后得到新点,记为2P = P + P,同理可扩展出3P = 2P + P、kP(k为正整数)。
3.安全核心:离散对数问题
ECC的安全性依赖于“椭圆曲线上的离散对数问题”的难解性:
已知椭圆曲线上的点P和kP(k为私钥,是一个随机大整数),要反向计算出k,在现有计算机技术下几乎不可能——即使使用超级计算机,破解256位ECC密钥也需要数百万年,而相同安全级别下,RSA密钥需要3072位,破解难度更低。
三、ECC的核心优势:为何能替代RSA?
相比传统的RSA、DSA等非对称加密算法,ECC的优势集中在“效率”和“资源适配性”上,这使其成为资源受限场景的首选。
在密钥长度方面,当需要达到128位安全级时,椭圆曲线加密(ECC)仅需256位的密钥,而RSA(传统非对称加密)则需要3072位的密钥,两者安全强度相当,但ECC密钥长度仅为RSA的约1/12,更易存储和管理。计算效率上,ECC的加密与解密速度比RSA快3-5倍,尤其在高频次加密场景(如海量物联网设备数据上传)中,能显著减少等待时间。带宽占用层面,由于ECC密钥更短,加密后的数据在网络传输时产生的数据量更小,可降低移动网络、窄带物联网等低带宽场景的传输成本。资源消耗上,ECC对CPU算力和内存的占用更少,能适配智能手机、智能传感器等硬件资源有限的设备,避免设备因运算压力过大出现卡顿或断电;而RSA占用资源较多,在这类设备上长期运行易导致性能过载。
四、应用场景与具体案例
如今ECC已渗透到数字生活的多个关键领域,其“高效安全”的特性在具体场景中展现出显著价值,以下为不同领域的实际应用案例:
1.移动支付与金融领域
移动支付的核心需求是“快速验证+防篡改”,ECC能完美满足这一需求。以微信支付为例,用户在扫码付款时,手机端会通过ECC生成临时交易签名,该签名仅包含256位密钥相关信息,体积远小于RSA签名。签名传输到微信支付服务器后,服务器用对应的公钥进行验证,整个过程耗时不足0.1秒,既避免了网络延迟影响支付体验,又能通过ECC的数学特性防止签名被篡改——即使攻击者截获签名,也无法反向推导出私钥,确保用户账户资金安全。此外,中国银联的“云闪付”APP中,用户绑定银行卡时的身份认证环节,也采用ECC对银行卡信息进行加密,防止信息在传输中泄露。
2.物联网(IoT)领域
物联网设备普遍存在“算力低、存储小、功耗有限”的特点,ECC的轻量级特性使其成为该领域的首选加密方案。以智能电表为例,某电力公司部署的智能电表采用ARM Cortex-M0内核芯片,内存仅8KB,无法承载RSA 3072位密钥的运算。采用256位ECC密钥后,智能电表每天可完成1440次用电数据加密(每小时1次),加密过程仅消耗0.3mAh电量,不会额外增加电表的供电负担;同时,加密后的用电数据通过窄带物联网(NB-IoT)网络上传时,单条数据大小比RSA加密小60%,每月可减少约50MB的流量消耗,降低运营成本。此外,智能门锁的指纹数据本地加密、共享单车的开锁指令签名,也均采用ECC技术。
3.区块链技术领域
区块链的核心需求是“资产归属唯一+交易不可篡改”,ECC是实现这一需求的基础技术。以比特币为例,用户创建比特币钱包时,系统会通过ECC生成一对密钥:私钥是一个随机的256位整数(类似“数字钥匙”),公钥由私钥通过椭圆曲线点运算生成,钱包地址则是公钥经过哈希处理后的字符串。当用户向他人转账比特币时,需用私钥对交易信息(转账金额、接收地址等)进行签名,签名会随交易信息一起广播到比特币网络。全网节点收到交易后,用转账者的公钥验证签名合法性——只有私钥持有者能生成有效的签名,从而确认交易是资产所有者发起的,避免他人伪造转账。以太坊、莱特币等其他区块链项目,也均采用ECC作为核心签名技术。
4.HTTPS协议与网页安全
HTTPS的核心是通过SSL/TLS证书实现“网站身份验证+数据加密传输”,ECC能提升HTTPS的运行效率。全球知名证书机构Let's Encrypt已将ECC证书作为默认选项,某电商平台将网站SSL证书从RSA 2048位升级为ECC 256位后,服务器处理HTTPS请求的并发量提升了40%——原来每台服务器每秒可处理800个HTTPS请求,升级后可处理1120个,减少了服务器集群的扩容成本。对用户而言,访问该电商网站时,SSL握手时间从150ms缩短至80ms,网页加载速度明显提升,尤其在4G、5G移动网络环境下,用户无需等待过长时间即可打开网页。目前,Chrome、Safari、Edge等主流浏览器均已全面支持ECC证书,全球Top 1000网站中约60%已采用ECC证书。
五、ECC的挑战与未来
尽管ECC目前是主流加密技术,但仍面临两大潜在挑战:
1.侧信道攻击风险:ECC的运算过程可能泄露“时间、功耗”等侧信道信息,攻击者可通过分析这些信息反推私钥。例如,某智能卡若未优化ECC运算逻辑,在执行倍点操作时,不同数值对应的运算时间不同,攻击者可通过记录运算时间,逐步缩小私钥的可能范围。目前行业已通过“随机化运算顺序”“恒定时间实现”等技术规避这一风险——让ECC运算无论处理何种数据,都保持相同的时间和功耗,切断侧信道信息与私钥的关联。
2.量子计算威胁:量子计算机的“肖尔算法”可高效解决离散对数问题,若大规模量子计算机(如具备数千个量子比特的设备)落地,现有ECC的安全性将受到冲击。目前,国际标准化组织(ISO)和美国国家标准与技术研究院(NIST)已启动“后量子加密技术”的标准化工作,研究基于格基、哈希、基于码等数学难题的加密算法,这些算法能抵抗量子计算攻击。未来,后量子加密技术可能与ECC形成互补——在量子计算机未普及前,继续使用ECC保障安全;量子计算机落地后,逐步过渡到后量子加密体系。
总结
椭圆曲线加密技术凭借“短密钥、高安全、低消耗”的特性,解决了传统非对称加密在资源受限场景中的痛点,成为数字安全的“基础设施”。从微信支付的毫秒级签名验证,到智能电表的低功耗数据加密,从比特币的资产归属确认,到电商网站的快速HTTPS加载,ECC正在默默守护每一次数字交互的安全,也是未来数字世界安全体系的重要组成部分。