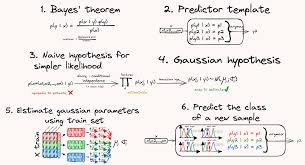
朴素贝叶斯算法,作为基于贝叶斯定理的简洁概率分类器,其名称中的“朴素”二字源自其对特征之间独立性的强烈假设,尽管这一假设在现实世界的复杂数据中往往难以严格满足,但朴素贝叶斯仍能在诸多场景下展现出卓越的分类性能。接下来,我们将深入探讨该算法的核心原理、工作流程、变种形式及其在实际应用中的优缺点。
一、贝叶斯定理:朴素贝叶斯算法的基石
朴素贝叶斯算法的核心驱动力源于贝叶斯定理,这一定理揭示了在已知某种条件下的事件A发生概率(后验概率)与无条件事件A发生的概率(先验概率)、以及条件B在事件A发生时的概率之间的关系。数学表达式如下:
\\[ P(A|B) = \\frac{P(B|A) \\cdot P(A)}{P(B)} \\]
其中,\\( P(A|B) \\)代表在事件B发生的条件下事件A发生的概率;\\( P(B|A) \\)是在事件A发生的条件下事件B发生的概率;\\( P(A) \\)是事件A的先验概率;\\( P(B) \\)是事件B的总概率。
二、朴素贝叶斯分类器:基于概率的决策机制
朴素贝叶斯分类器运用贝叶斯定理来估算在给定一组输入特征的情况下,一个实例属于某一特定类别的概率。对于分类任务而言,关键在于计算条件概率 \\( P(C_k|x_1, x_2, ..., x_n) \\),即在特征集 \\( x_1, x_2, ..., x_n \\) 已知的前提下,实例归属于类别 \\( C_k \\) 的概率。依据朴素贝叶斯假设,各特征间相互独立,故此概率可简化为:
\\[ P(C_k|x_1, x_2, ..., x_n) = \\frac{P(C_k) \\cdot \\prod_{i=1}^{n} P(x_i|C_k)}{P(x_1, x_2, ..., x_n)} \\]
此处,分母 \\( P(x_1, x_2, ..., x_n) \\) 对所有类别而言相同,因此在分类决策过程中可以忽略不计。
三、实施朴素贝叶斯算法的步骤
要成功运用朴素贝叶斯算法进行分类任务,需遵循以下步骤:
1. 收集数据:积累足够数量且质量良好的数据集,用于训练分类器。
2. 准备数据:对原始数据进行必要的预处理,如对文本数据进行分词、去除停用词、标准化等操作,使之适应算法要求。
3. 分析数据:探究数据的分布特性,为每一个类别计算其先验概率 \\( P(C_k) \\)。
4. 估计概率:针对每个类别,计算在该类别下各特征出现的概率 \\( P(x_i|C_k) \\)。这一步骤可能涉及频率统计、最大似然估计或贝叶斯估计等方法。
5. 分类新数据:对于新的待分类实例,计算其属于各个类别的概率,并选取最高概率对应的类别作为最终预测结果。
四、朴素贝叶斯的变体:适应不同数据类型的实现
针对不同类型的输入数据,朴素贝叶斯算法衍生出多种变体以适应各自的特点:
● 多项式朴素贝叶斯:特别适用于处理分类文本数据,采用多项式分布来估计特征概率,考虑了特征在文档中出现的次数。
● 伯努利朴素贝叶斯:同样应用于文本分类,但假设文本数据由伯努利分布生成,即每个词的出现与否被视为独立的二元事件。
● 高斯朴素贝叶斯:适用于特征值符合正态分布的情形,此时特征概率通过高斯分布(即正态分布)来估计。
五、朴素贝叶斯算法的优点与局限性
优点:
● 算法简单:朴素贝叶斯算法逻辑清晰、实现便捷,易于理解和调试。
● 高效处理大数据:由于其计算过程主要涉及简单的概率乘积与求和,故在处理大规模数据时表现出较高的效率。
● 在满足特征独立假设时效果出色:当数据特征确实近似独立时,朴素贝叶斯分类器能实现高度准确的分类。
缺点:
● 特征独立性假设的局限性:现实生活中的数据特征往往存在不同程度的相关性,朴素贝叶斯的强独立性假设可能导致分类性能的下降。
● 对概率估计的准确性依赖性强:算法的分类效果很大程度上取决于概率估计的准确性,而这通常需要大量的数据支持。
六、朴素贝叶斯在实际应用中的实例
朴素贝叶斯算法因其高效、简洁的特性,在众多领域得到广泛应用。以下列举几个典型应用场景:
1. 垃圾邮件过滤:朴素贝叶斯分类器通过对邮件内容进行细致分析,学习垃圾邮件特有的词汇、短语等特征,进而用于判断新邮件是否为垃圾邮件。在实际操作中,算法会计算邮件属于垃圾邮件和非垃圾邮件的概率,并据此进行分类决策。
2. 情感分析:在情感分析任务中,朴素贝叶斯算法通过对文本数据(如产品评论、社交媒体帖子等)的深入剖析,确定作者的情感倾向(如正面、负面或中性)。算法依据文本中蕴含的情感特征词汇来计算情感倾向的概率,并据此进行情感分类。
3. 文本分类:朴素贝叶斯算法在文本分类任务中大放异彩,能够自动将文本文档归入预定义的类别中,如新闻文章的主题分类、文档的文件夹归类等。算法将文本转化为特征向量,并基于这些特征进行概率计算与分类。
尽管朴素贝叶斯算法在特征独立性假设上存在一定的理想化,但在实际应用中,其凭借贝叶斯定理的强大理论基础、高效的计算能力以及对大规模数据的良好适应性,依然在诸多领域展现出强大的实用性。通过引入更先进的特征表示方法(如Word2Vec、BERT等)或集成学习策略,可以进一步提升朴素贝叶斯分类器的泛化能力和预测精度,使其在面对复杂数据挑战时保持竞争力。