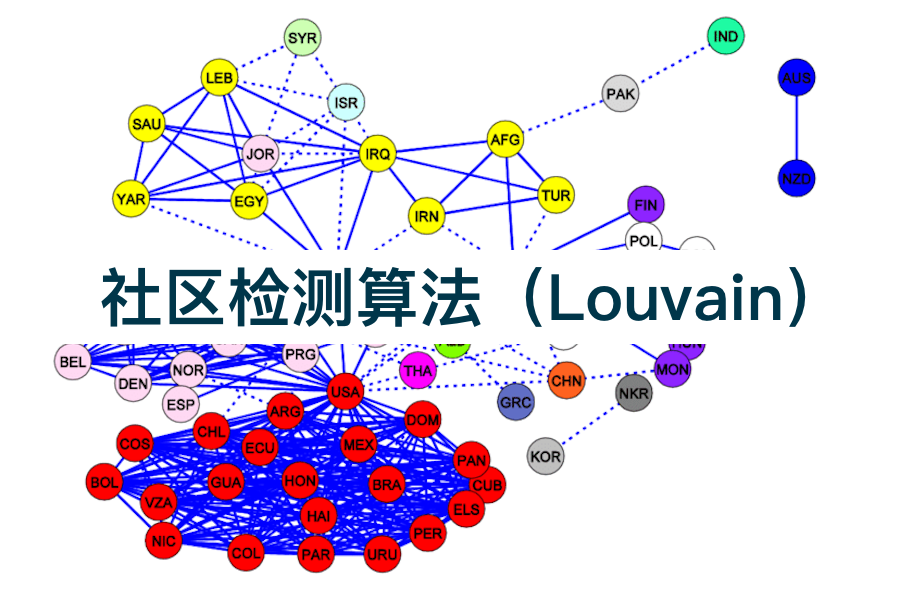
Louvain算法是一种经典的社区检测(community detection)算法,从复杂网络中识别出紧密连接的子群体(即“社区”),其核心目标是最大化模块度(modularity)——一种衡量网络社区划分质量的指标。该算法由Blondel等人于2008年提出,因效率高、适合大规模网络而被广泛应用。
一、基本概念
Louvain算法其实就是一种帮我们在复杂网络里“找小团体”的工具,说直白点,就像在一堆互相有联系的人中,快速找出那些“抱团最紧”的小圈子。
举个最常见的例子:比如你们学校的微信好友网络——每个人是一个点,加了好友就用线连起来。这时候你会发现,有些小圈子特别明显:比如篮球队的男生们互相都是好友,和其他同学的联系就少;班里的女生闺蜜团也是,内部互动频繁,对外连接稀疏。Louvain算法干的就是自动找出这些“内部特亲、外部较疏”的小圈子。
它怎么找呢?就像玩一个“优化小圈子”的游戏,分两步反复做,直到找不到更好的小圈子为止:
第一步:每个点先自己算一个“小圈子”(就像每个人先自己当一个小团体)。然后挨个看每个点:“我要是加入隔壁那个小圈子,会不会让我们俩的小圈子更抱团?” 比如你发现加入同桌的小圈子后,大家互相加好友的比例更高了(更抱团),那就加入;如果没好处,就待在原来的圈子里。所有人都这么试一遍,直到没人想动了,这一步就结束。
第二步:把第一步里形成的小圈子“打包”成一个个“超级点”。比如篮球队5个人形成了一个小圈子,就把他们看成一个“篮球大团体”;闺蜜团4个人看成一个“闺蜜大团体”。然后在这些“大团体”之间再连线(比如篮球团和闺蜜团里有人是好友,就给这两个大团体连一条线),形成一个新的“大团体网络”。
之后,就用这个新的大团体网络,再重复第一步和第二步:看看大团体之间能不能再合并成更大的圈子,直到怎么调整都没法让整个网络的“抱团程度”更好为止。
这个算法的好处很明显:
特别快,就算有上百万人的网络(比如整个微信的好友关系),它也能很快算出结果;
不用提前告诉它“要找多少个小圈子”,它自己能算出最合适的数量。
当然也有小缺点:比如有时候会错过特别小的小圈子(比如只有2个人的秘密好友),而且一个人只能属于一个圈子(不能同时在两个小团体里)。
总的来说,Louvain就像一个“网络侦探”,能在乱糟糟的关系网里,快速揪出那些藏得深但联系紧密的小团体——不管是社交网络里的兴趣群、班级里的小团伙,还是细胞里合作干活的蛋白质小组,它都能搞定。
二、核心目标
社区检测的本质是发现网络中“内部连接密集、外部连接稀疏”的子结构。模块度(用Q表示)正是量化这种结构的指标,它通过比较网络中实际的边连接情况与随机情况下的预期连接情况,来评估社区划分的优劣。具体来说,它会考量节点间是否存在实际连接、节点的度数(连接边数)、网络总边数,以及节点是否属于同一社区等因素,最终输出一个衡量社区内连接紧密程度相对于随机连接的指标。模块度Q的取值范围为[-1/2, 1],值越大说明社区划分越显著(通常Q>0.3即认为存在有效社区)。
三、算法步骤
Louvain算法通过局部优化+社区聚合的迭代过程实现模块度最大化,具体分为两个核心阶段,重复执行直到模块度不再提升:
阶段1:局部优化(节点归属调整)
1.初始状态:每个节点单独作为一个社区(即每个社区仅含1个节点)。
2.遍历每个节点$i$,计算将其从当前社区移动到每个邻居节点$j$所在社区时,模块度的变化量$\\Delta Q$。
3.若最大\\(\\Delta Q > 0\\),,则将节点$i$移动到对应邻居的社区(选择$\\Delta Q$最大的社区);否则保持原社区。
4.重复步骤2-3,直到所有节点的归属不再变化(局部稳定)。
阶段2:社区聚合(构建超级节点)
1.将阶段1中形成的每个社区视为一个“超级节点”(super node)。
2.构建新网络:超级节点之间的边权重为原社区内所有节点间边的权重之和(若原网络为无权重网络,则计数边的数量)。
3.以新网络为输入,重复阶段1和阶段2,直到模块度无法再提升。
四、优点:为什么大家常用它?
1.速度快,能扛住“大数据”
它对大规模网络特别友好,哪怕网络里有上百万个节点(比如整个城市的社交关系网),也能在短时间内算出结果。这比很多只能处理几千个节点的算法实用多了。
2.不用“猜答案”,全自动划分
用的时候不用提前告诉它“要找多少个社区”,算法会自己根据网络的实际情况,算出最合适的社区数量。比如分析班级好友网时,不用手动设定“分3个还是5个圈子”,它会自动找到最合理的划分。
3.结果“抱团感”强,符合直觉
它的核心是优化“模块化”(可以理解为“圈子紧密程度的打分”),最后得到的社区往往内部连接特别密、外部连接特别疏,和我们直观感受的“小圈子”很吻合。比如篮球队的圈子和闺蜜团的圈子,划分后边界很清晰。
4.步骤简单,容易理解和实现
算法逻辑不复杂(先拆成小圈子,再合并成大圈子,反复优化),普通人也能看懂大概原理,工程师实现起来也不麻烦,所以应用很广。
五、缺点:哪些场景它可能“失灵”?
1.对“小圈子”不敏感,容易漏检
它有个“分辨率限制”:如果社区规模很小(比如只有3-5个人的小团体),算法可能会把它们当成大圈子的一部分,检测不出来。比如班级里有个偷偷成立的“游戏三人组”,可能被算法算进“男生大圈子”里,没法单独识别。
2.可能“走弯路”,找不到最优解
算法有时候会陷入“局部最优”——就像找路时,找到一条还不错的近路就停下了,但其实还有一条更近的路没发现。所以有时候换个初始状态(比如第一次算从A节点开始,第二次从B节点开始),得到的社区划分可能不一样。
3.“非黑即白”,容不下“脚踏两条船”
它只能做“硬划分”:一个节点只能属于一个社区,没法处理“重叠社区”。但现实中很多人会同时属于多个圈子(比如一个人既是篮球队成员,又是学习小组成员),这时候算法就会“强行”把他归到其中一个,不够灵活。
4.对“关系强度”敏感,权重设不好容易错
如果网络里的边有权重(比如好友间的互动次数:点赞1次算1分,评论1次算3分),权重设置得不合理会直接影响结果。比如把“点赞”权重设太高,可能会把偶尔点赞的“泛泛之交”算进紧密圈子里。
5.可能“过度合并”,把该分开的圈子捆在一起
有时候两个其实应该分开的圈子(比如两个互相不太来往的班级),可能因为中间有几个人互相认识,被算法强行合并成一个大圈子,导致划分不够精准。
六、应用场景
Louvain算法因能高效处理大规模网络、自动识别“内部连接紧密、外部连接稀疏”的社区结构,在多个领域有广泛应用,其核心价值是通过挖掘网络的隐含子结构,解决实际场景中的分析、预测或优化问题。
1.社会网络分析
社交平台用户群体识别:在Facebook、Twitter、微信等社交网络中,Louvain可自动识别“兴趣社群”(如母婴群体、游戏爱好者)、“好友圈子”(如同学圈、同事圈)或“传播社群”(如某类信息的主要传播群体)。例如:通过用户间的好友关系、互动频率(点赞、评论)构建网络,Louvain能快速划分出紧密互动的子群体,帮助平台定向推送内容、管理社群关系。
舆情传播追踪:在舆情事件中,通过分析用户转发、评论关系形成的网络,Louvain可识别出“核心传播社区”(如意见领袖及其紧密追随者),预测舆情扩散路径,辅助舆情管控。
2.生物与医学网络
蛋白质相互作用(PPI)网络分析:蛋白质通过相互作用形成复杂网络,Louvain可识别其中的“功能模块”(如参与同一代谢通路或疾病调控的蛋白质集群)。例如:在癌症相关PPI网络中,通过社区检测发现与肿瘤发生密切相关的蛋白质模块,为靶向药物研发提供候选靶点。
基因调控网络分析:基因间的调控关系(如转录因子与靶基因的相互作用)可构成网络,Louvain能划分出协同表达的基因社区,帮助理解细胞功能(如胚胎发育、免疫反应)的分子机制。
3.推荐系统优化
用户/物品社区匹配:在电商(如亚马逊)、视频平台(如Netflix)中,通过用户-物品交互网络(如购买、观看记录),Louvain可同时划分“用户社区”(兴趣相似的用户群体)和“物品社区”(功能/类型相近的商品/视频)。同一社区内的用户对社区内物品的偏好更一致,基于此可实现精准推荐(如给“科幻电影社区”用户推荐同社区的新科幻片)。
冷启动问题缓解:新用户/物品可通过其初始少量交互,被分配到相似的社区中,利用社区整体偏好进行推荐,减少“数据稀疏”带来的影响。
4.交通与城市规划
城市交通网络分析:在地铁网络、公交网络或道路网络中,Louvain可识别“紧密连通的区域社区”(如市中心核心区、郊区卫星城)。例如:通过地铁站点间的换乘关系构建网络,社区划分结果可辅助优化公交线路覆盖(如为跨社区的薄弱连接增加班次)、规划城市功能区(如将商业设施集中在高互动社区)。
人流移动模式挖掘:基于手机信令数据(用户在区域间的移动轨迹)构建网络,Louvain可识别“通勤社区”(如居住-工作的高频流动区域),为城市职住平衡、基础设施布局提供依据。
5.金融与风控
欺诈团伙识别:在金融交易网络中(节点为账户,边为交易关系),欺诈账户往往通过频繁交易形成紧密社区(如洗钱团伙、虚假交易账户)。Louvain可快速定位这类高互动社区,辅助风控系统识别异常交易群体,降低金融风险。
信贷关联风险分析:在借贷网络中(节点为企业/个人,边为担保、联保关系),社区划分可识别“风险关联圈”(如互保的企业集群),当圈内某一主体违约时,可预警整个社区的连锁风险。
6.学术与合作网络
科研团队识别:通过学者间的论文合作关系网络,Louvain可划分出“研究社区”(如某一细分领域的核心合作团队),分析学科交叉趋势(如不同社区间的连接强度反映跨领域合作活跃度),或辅助科研资源分配(如向高产社区倾斜 funding)。
文献/专利聚类:基于文献引用关系、专利共被引关系构建网络,Louvain可将主题相关的文献/专利聚为社区,帮助研究者快速定位某一领域的核心成果。
结言
Louvain算法的核心应用逻辑是:通过挖掘网络中“隐性的紧密子结构”,将复杂网络简化为可解释的社区单元,从而实现从“整体混沌”到“局部有序”的分析。其高效性使其尤其适合百万级节点的大规模网络,因此在需要处理海量连接数据的场景(如社交、生物、交通)中表现突出。